
【题目】现在颈椎病患者越来越多,甚至大学生也出现了颈椎病,年轻人患颈椎病多与工作、生活方式有关,某调查机构为了了解大学生患有颈椎病是否与长期过度使用电子产品有关,在遂宁市中心医院随机的对入院的50名大学生进行了问卷调查,得到了如下的4×4列联表:
未过度使用 | 过度使用 | 合计 | |
未患颈椎病 | 15 | 5 | 20 |
患颈椎病 | 10 | 20 | 30 |
合计 | 25 | 25 | 50 |
(1)是否有99.5%的把握认为大学生患颈锥病与长期过度使用电子产品有关?
(2)已知在患有颈锥病的10名未过度使用电子产品的大学生中,有3名大学生又患有肠胃炎,现在从上述的10名大学生中,抽取3名大学生进行其他方面的排查,记选出患肠胃炎的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据与公式:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
科目:高中数学 来源: 题型:
【题目】某车间20名工人年龄数据如下表:
年龄(岁) | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合计 |
工人数(人) | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
(1)求这20名工人年龄的众数与平均数;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)是否存在整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上存在极小值,若存在,求出所有整数
上存在极小值,若存在,求出所有整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
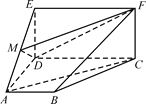
【题目】如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,![]() ,M是线段AE上的动点.
,M是线段AE上的动点.
(1)试确定点M的位置,使AC∥平面DMF,并说明理由;
(2)在(1)的条件下,求平面DMF与平面ABCD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的产品中抽取1000件测量这些产品的一项质量指标值,由测量结果得到频率分布直方图如图所示.
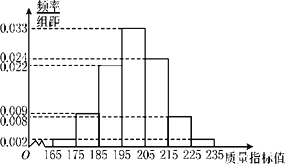
(Ⅰ)求这1000件产品质量指标值的样本平均数![]() 和样本方差s2(同一组数据用该区间的中点值作代表).
和样本方差s2(同一组数据用该区间的中点值作代表).
(Ⅱ)由频率分布直方图可以认为这种产品的质量指标值Z服从正态分布N(μ,δ2),其中μ近似为样本平均数![]() ,δ2近似为样本方差s2.
,δ2近似为样本方差s2.
![]() 利用该正态分布,求P(175.6<Z<224.4);
利用该正态分布,求P(175.6<Z<224.4);
②某用户从该企业购买了100件这种产品,估计其中质量指标值位于区间(175.6,224.4)的产品件数.(精确到个位)
附: ![]() ≈12.2,若Z~N(μ,δ2),则P(μ-δ<Z<μ+δ)=0.6826,
≈12.2,若Z~N(μ,δ2),则P(μ-δ<Z<μ+δ)=0.6826,
P(μ-2δ<Z<μ+2δ)=0.9544
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年春节期间,某服装超市举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.
方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现从中随机抽取100人的数学与地理的水平测试成绩如下表:
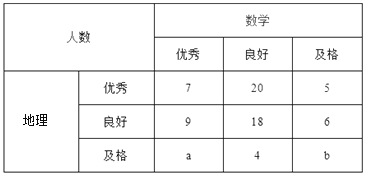
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有![]() .
.
(Ⅰ)若在该样本中,数学成绩优秀率是30%,求![]() 的值;
的值;
(Ⅱ)已知![]() ,求数学成绩为优秀的人数比及格的人数少的概率.
,求数学成绩为优秀的人数比及格的人数少的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com