练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图所示，半圆⊙O的直径为2，A为直径MN延长线上一点，且OA＝2，B为半圆周上任一点，以AB为边作等边△ABC(A、B、C按顺时针方向排列)，问∠AOB为多少时，四边形OACB的面积最大？最大面积是多少？

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图所示，半圆O的直径为2，A为半圆直径的延长线上的一点，且OA=2，B为半圆上任一点，以AB为边作等边△ABC，问B在什么地方时，四边形OACB的面积最大？并求出这个面积的最大值．
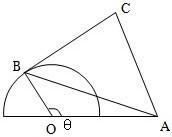
    精英家教网

    查看答案和解析>>

    科目：高中数学 来源： 题型：

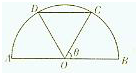    农户计划将已有的一块半径为100米的土地（如图所示）重新规划，拟将面积相等的两个△AOD与△BOC置为普通花草地，△COD置为特级花草地，O为半圆圆心，∠COB=θ，据市场调查，特级花草市场销售价变化不大，普通花草市场销售价变化较大，以往经验显示：特级花草地每平方米年利润为a元，普通花草地每平方米年利润为asinθ元．
    （1）分别写出△BOC、△AOD、△COD的面积关于θ的函数关系；
    （2）写出农户年总利润f（θ）关于θ的函数关系，当θ为何值时，年总利润f（θ）最大．

    查看答案和解析>>

    科目：高中数学 来源：2011年高三数学精品复习10：定比分点、平移、正余弦定理（解析版） 题型：解答题

    如图所示，半圆O的直径为2，A为半圆直径的延长线上的一点，且OA=2，B为半圆上任一点，以AB为边作等边△ABC，问B在什么地方时，四边形OACB的面积最大？并求出这个面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源：1977年上海市高考数学试卷（理科）（解析版） 题型：解答题

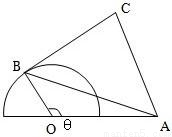
    如图所示，半圆O的直径为2，A为半圆直径的延长线上的一点，且OA=2，B为半圆上任一点，以AB为边作等边△ABC，问B在什么地方时，四边形OACB的面积最大？并求出这个面积的最大值．

    查看答案和解析>>

    同步练习册答案