
如图 是一个斜三棱柱,已知
是一个斜三棱柱,已知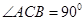 、平面
、平面 平面
平面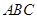 、
、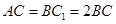 、
、 ,又
,又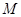 、
、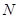 分别是
分别是 、
、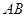 的中点.
的中点.

(1)求证: ∥平面
∥平面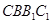 ; (2)求二面角
; (2)求二面角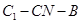 的大小.
的大小.
(1)详见解析;(2)二面角 的大小是
的大小是 .
.
【解析】
试题分析:(1)证明线面平行,有两种思路,一是证线面平行,二通过面面平行来证明.在本题中,两种思路比较,可以看出,取AC的中点P,证明平面MPN∥平面 是很容易的.
是很容易的.

(2)首先作出二面角的平面角. 由于平面 平面
平面 ,所以过C1作BC的垂线,则该垂线垂直于面BCN.因为
,所以过C1作BC的垂线,则该垂线垂直于面BCN.因为 、
、 、
、 ,∴
,∴  ⊥
⊥ ,
,
从而  ⊥平面
⊥平面 .
.
再过点B作BO⊥CN于O、连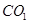 ,则
,则 ⊥CN
⊥CN
所以∠ 是二面角
是二面角 的一个平面角.在
的一个平面角.在 中,求出即可∠
中,求出即可∠ .
.
试题解析:(1)取AC的中点P,连MP、NP。易证MP∥ 、NP∥BC,所以平面MPN∥平面
、NP∥BC,所以平面MPN∥平面 ,得MN∥平面
,得MN∥平面 4分
4分

(2)设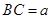 ,则
,则 、
、 、
、
∴  ⊥
⊥ 5分
5分
∴  ⊥平面
⊥平面 6分
6分
过点B作BO⊥CN于O、连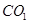 ,则
,则 ⊥CN
⊥CN
所以∠ 是二面角
是二面角 的一个平面角 9分
的一个平面角 9分
又易求 ,得
,得
 ,即
,即 11分
11分
也即二面角 的大小是
的大小是 12分
12分
考点:1、直线与平面平行;2、二面角.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
 如图,△A′B′C′是水平放置的△ABC的斜二测直观图,其中O′C′=O′A′=1,O′B′=
如图,△A′B′C′是水平放置的△ABC的斜二测直观图,其中O′C′=O′A′=1,O′B′=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
在一个几何体的三视图中,正视图和俯视图是全等的矩形如图所示,则这个几何体可以为:①斜三棱柱;②四棱柱;③圆柱
其中真命题的个数是

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com