

(1)请写出求方程ax2+(a+1)x+1=0根的算法;
(2)本题中给出的程序框图解决这个问题正确吗?它表达的是哪一个问题的算法框图?
(3)根据(1)重新绘制解决该问题算法的程序框图.
解析:本问题里a的值没有限制,因而必须分a=0和a≠0两种情形讨论,当a=0时,方程的根为x=-1;当a≠0时,方程有两根x1=-1,x2=-1/a.因此在画程序框图时,必须使用条件分支结构.
(1)求方程ax2+(a+1)x+1=0根的算法如下:
第一步:输入a;
第二步:如果a=0,则x=-1,并输出x,否则,执行第三步;
第三步:当a≠0时,x1=-1,x2=-1/a;
第四步:输出x1,x2.
(2)本题中给出的程序框图解决这个问题不正确.因为它没有体现出对a的取值的判断,没有应用判断框,没有用上条件分支结构,使求解结果错误,这只是解决了算法中的一部分.
(3)根据(1)中给出的步骤,可以画出如下图所示的正确的算法程序框图:



 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:022
填空
(1)
如下图所示的算法功能是___________________________;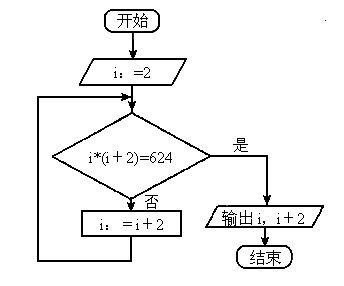
(2)
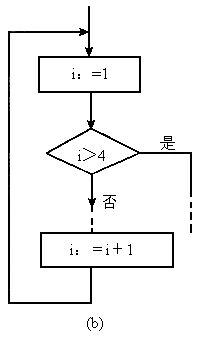
下图(a)是某循环框图的一部分,若改为图(b),则运行过程中出现的结果是__________.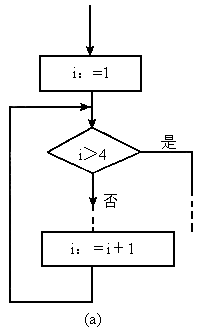
查看答案和解析>>
科目:高中数学 来源:专项题 题型:填空题
查看答案和解析>>
科目:高中数学 来源:同步题 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com