练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．设a=log73，$b={log_{\frac{1}{3}}}7$，c=30.7，则a，b，c的大小关系是（　　）
    A．a＜b＜cB．c＜b＜aC．b＜c＜aD．b＜a＜c

    分析 利用指数函数和对数函数的单调性求解．

    解答 解：0=log71＜a=log73＜log77=1，
    $b={log_{\frac{1}{3}}}7$＜$lo{g}_{\frac{1}{3}}1$=0，
    c=30.7＞30=1，
    ∴b＜a＜c．
    故选：D．

    点评 本题考查三个数的大小的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．半径为1，圆心角为$\frac{2}{3}π$的扇形卷成一个圆锥，则它的体积为（　　）
    A．$\frac{{2\sqrt{2}π}}{81}$B．$\frac{{2\sqrt{2}π}}{27}$C．$\frac{π}{27}$D．$\frac{π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．给出下列命题：
    ①存在实数α，使sinα•cosα=$\frac{1}{3}$；
    ②函数y=sin4x-cos4x的最小正周期是π；
    ③设$\overrightarrow a，\overrightarrow b$是两个非零向量，若存在实数λ，使$\overrightarrow b$=λ$\overrightarrow a$，则|$\overrightarrow a$+$\overrightarrow b$|=|$\overrightarrow a$|-|$\overrightarrow b$|；
    ④若sin（2x1-$\frac{π}{4}$）=sin（2x2-$\frac{π}{4}$），则x1-x2=kπ，其中k∈Z；
    ⑤若α、β是第一象限的角，且α＞β，则sinα＞sinβ．
    其中正确命题的序号是①②．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

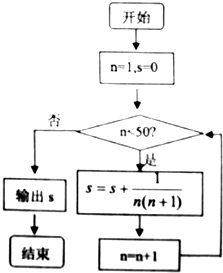    8．某算法的程序框图如图所示，则执行该算法后输出的结果为（　　）
    A．$\frac{39}{40}$B．$\frac{49}{50}$C．$\frac{50}{49}$D．$\frac{60}{59}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知tanα=2，则sinαcosα+2cos2α=$\frac{4}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知△ABC的面积为$\frac{{4\sqrt{3}}}{3}$，AC=3，B=60°，则△ABC的周长为8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．在下列向量组中，可以把向量$\overrightarrow a$=（-3，7）表示出来的是（　　）
    A．$\overrightarrow{e_1}=（0，1），\overrightarrow{e_2}=（0，-2）$B．$\overrightarrow{e_1}=（1，5），\overrightarrow{e_2}=（-2，-10）$
    C．$\overrightarrow{e_1}=（-5，3），\overrightarrow{e_2}=（-2，1）$D．$\overrightarrow{e_1}=（7，8），\overrightarrow{e_2}=（-7，-8）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．下列结论错误的是（　　）
    A．命题“若p，则q”与命题“若￢q，则￢p”互为逆否命题
    B．命题p：“?x∈[0，1]，1≤ex≤e”（e是自然对数的底数），命题q：“?x∈R，x2+x+1＜0”，则p∨q为真
    C．“am2＜bm2”是“a＜b”成立的必要不充分条件
    D．若p∨q为假命题，则p、q均为假命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知a=2${\;}^{-\frac{1}{2}}$，b=log${\;}_{\frac{1}{3}}$2，c=log${\;}_{\frac{1}{2}}$$\frac{1}{5}$，则（　　）
    A．a＞b＞cB．a＞c＞bC．c＞a＞bD．c＞b＞a

    查看答案和解析>>

    同步练习册答案