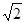Question

（本小题满分10分）设圆满足：
(Ⅰ)截y轴所得弦长为2；
(Ⅱ)被x轴分成两段圆弧，其弧长的比为3∶1．
在满足条件(Ⅰ)、(Ⅱ)的所有圆中，求圆心到直线l:x-2y=0的距离最小的圆的方程.

Answer 1

解法一 设圆的圆心为P(a，b)，半径为r，则点P到x轴，y轴的距离分别为|b|，|a|。由题设知圆P截x轴所得劣弧所对的圆心角为90°，∴圆P截x轴所得的弦长为r，故r²=2b²。 又圆P截y轴所得的的弦长为2，所以有r²=a²+1。从而得2b²-a²=1。又点P(a，b)到直线x-2y=0的距离为d=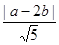，所以5d²=|a-2b|²=a²+4b²-4ab≥a²+4b² -2(a²+b²)=2b²-a²=1，当且仅当a=b时，上式等号成立，从而要使d取得最小值，则应有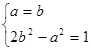，解此方程组得或。又由r²=2b²知r=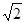。于是，所求圆的方程是(x-1)²+(y-1)²=2或(x+1)²+(y+1)²=2。------10分
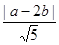解法二 同解法一得d=，∴a-2b=±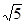d，得a²=4b²±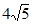bd+5d²     ①
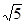将a²=2b²-1代入①式，整理得2b²±4bd+5d²+1="0 " ② 把它看作b的二次方程，由于方程有实根，故判别式非负，即△=8(5d²-1)≥0，得5d²≥1。所以5d²有最小值1，从而d有最小值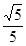。将其代入②式得2b²±4b+2=0，解得b=±1。将b=±1代入r²=2b²得r²=2，由r²=a²+1得a=±1。综上a=±1，b=±1，r²=2。由|a-2b|=1知a，b同号。于是，所求圆的方程是(x-1)²+(y-1)²=2或(x+1)²+(y+1)²=2。--------10分

略