
 本题共3个小题,第1、2小题满分各5分,第3小题满分6分.
本题共3个小题,第1、2小题满分各5分,第3小题满分6分.| S1 |
| S2 |
| atanθ |
| 1+tanθ |
| 1 |
| 2 |
| 1 |
| x |
| FG |
| AB |
| DG |
| DB |
| t |
| a |
| atanθ-t |
| atanθ |
| atanθ |
| 1+tanθ |
| 1 |
| 2 |
| a2tan2 θ |
| (1+tanθ)2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a2tan2θ |
| (1+tanθ)2 |
| S1 |
| S2 |
| (1+tanθ)2 |
| 2tanθ |
| b |
| a |
| 1 |
| 2 |
| 1 |
| x |
| b |
| a |
| π |
| 4 |
| b |
| a |
| b |
| a |
| 1 |
| 2 |
| 1 |
| x |
| b |
| a |
| 1 |
| 2 |
| b |
| a |
| a |
| b |


科目:高中数学 来源:2010年上海黄浦区高二下学期基础学业测评数学卷 题型:解答题
(本题满分10分)本题共3个小题,第1小题满分4分,第2小题满分3分,第3小题满分3分.
已知直线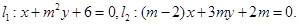 讨论当实数m为何值时,(1)
讨论当实数m为何值时,(1)
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分5分,第3小题满分9分.
已知数列![]() 是各项均为正数的等差数列,公差为d(d
是各项均为正数的等差数列,公差为d(d ![]() 0).在
0).在![]() 之间和b,c之间共插入
之间和b,c之间共插入![]() 个实数,使得这
个实数,使得这![]() 个数构成等比数列,其公比为q.
个数构成等比数列,其公比为q.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若插入的n个数中,有s个位于a,b之间,t个位于b,c之间,且![]() 都为奇数,试比较s与t的大小,并求插入的n个数的乘积(用
都为奇数,试比较s与t的大小,并求插入的n个数的乘积(用![]() 表示).
表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分5分,第3小题满分9分.
已知数列![]() 是各项均为正数的等差数列,公差为d(d
是各项均为正数的等差数列,公差为d(d ![]() 0).在
0).在![]() 之间和b,c之间共插入
之间和b,c之间共插入![]() 个实数,使得这
个实数,使得这![]() 个数构成等比数列,其公比为q.
个数构成等比数列,其公比为q.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求d的值;
,求d的值;
(3)若插入的n个数中,有s个位于a,b之间,t个位于b,c之间,且![]() 不都为奇数,试比较s与t的大小,并求插入的n个数的乘积(用
不都为奇数,试比较s与t的大小,并求插入的n个数的乘积(用![]() 表示).
表示).
查看答案和解析>>
科目:高中数学 来源:2009-2010学年上海市闵行区高一(下)期末数学试卷(解析版) 题型:解答题
 称为“草花比y”.
称为“草花比y”.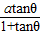 ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com