解:(Ⅰ)因为数列{a
n}为常数列,
所以a
n+1=a
n,
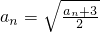
,
解得a
n=0或
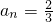
,
由n的任意性知,a
1=0或
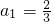
,
所以a=0,或
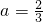
;
(Ⅱ)用数学归纳法证明
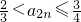
,
1当n=12时,
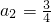
3,符合上式,
②假设当n=k(k≥1)时,
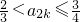
,
因为
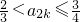
,
所以
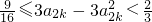
,
即
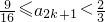
,
从而
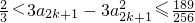
,
即
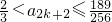
,
因为
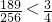
,
所以,当n=k+1时,

成立,
由①,②知,
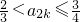
;
(Ⅲ)因为a
2n-a
2n-2=3(3a
2n-2-3a
2n-22)-3(3a
2n-2-3a
2n-22)
2-a
2n-2=-27a
2n-24+54a
2n-23-36a
2n-22+8a
2n-2(n≥2),
所以只要证明-27a
2n-24+54a
2n-23-36a
2n-22+8a
2n-2<0,
由(Ⅱ)可知,a
2n-2>0,所以只要证明-27a
2n-23+54a
2n-22-36a
2n-2+8<0,
即只要证明27a
2n-23-54a
2n-22+36a
2n-2-8>0,
令f(x)=27x
3-54x
2+36x-8,
f'(x)=27×3x
2-54×2x+36=9(9x
2-12x+4)=9(3x-2)
2≥0,
所以函数f(x)在R上单调递增,
因为
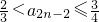
,所以
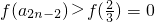
,
即27a
2n-23-54a
2n-22+36a
2n-2-8>0成立,
故a
2n<a
2n-2,
所以数列{a
2n}单调递减.
分析:(Ⅰ)由题意知a
n+1=a
n,
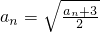
,由此可推导出a=0,或
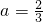
.
(Ⅱ)用数学归纳法证明
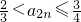
.
(Ⅲ)因为a
2n-a
2n-2=3(3a
2n-2-3a
2n-22)-3(3a
2n-2-3a
2n-22)
2-a
2n-2=-27a
2n-24+54a
2n-23-36a
2n-22+8a
2n-2(n≥2),
所以只要证明-27a
2n-24+54a
2n-23-36a
2n-22+8a
2n-2<0,然后用分析法能够证明数列{a
2n}单调递减.
点评:本题以数列为载体,考查不等式的证明,解题时要注意数列归纳法和分析法的证明技巧.

 ,求证:
,求证: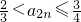 ;
;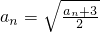 ,
,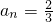 ,
,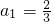 ,
,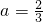 ;
;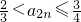 ,
,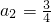 3,符合上式,
3,符合上式,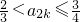 ,
,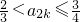 ,
,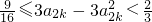 ,
,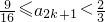 ,
,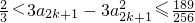 ,
,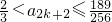 ,
,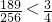 ,
, 成立,
成立,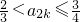 ;
;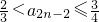 ,所以
,所以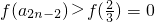 ,
,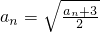 ,由此可推导出a=0,或
,由此可推导出a=0,或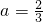 .
.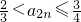 .
.

 阅读快车系列答案
阅读快车系列答案