
【题目】数学名著《算学启蒙》中有关于“松竹并生”的问题:松长四尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图,是源于其思想的一个程序框图.若输入的![]() 分别为8、2,则输出的
分别为8、2,则输出的![]() ( )
( )

A. 2 B. 3 C. 4 D. 5
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
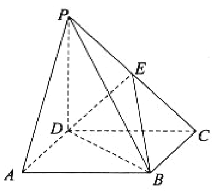
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一点.
上的一点.
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,三棱锥![]() 的体积是18,求
的体积是18,求![]() 点到平面
点到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年冬,北京雾霾天数明显减少,据环保局统计三个月的空气质量,达到优良的天数超过70天.重度污染的天数仅有4天.主要原因是政府对治理雾霾采取了有效措施,如①减少机动车尾气排放;②实施了煤改电或煤改气工程;③关停了大量的排污企业;④部分企业季节性的停产.为了解农村地区实施煤改气工程后天然气使用情况,从某乡镇随机抽取100户,进行均用气量调查,得到的用气量数据(单位:千立方米)均在区间![]() 围内,将数据按区间列表如下:
围内,将数据按区间列表如下:
分组 | 频数 | 频率 |
| 14 | 0.14 |
|
|
|
| 55 | 0.55 |
| 4 | 0.04 |
| 2 | 0.02 |
合计 | 100 | 1 |
(1)求表中![]() ,
,![]() 的值;
的值;
(2)若同组中的每个数据用该组区间中点值代替,估计该乡每户月平均用气量;
(3)从用量高于3千立方米的用户中任选2户,进行燃气使用的满意度调查,求这2户用气量处于不同区间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 图象上所有点的横坐标缩短为原来的
图象上所有点的横坐标缩短为原来的![]() ,纵坐标不变,再向右平移
,纵坐标不变,再向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则下列说法正确的是( )
的图象,则下列说法正确的是( )
A. 函数![]() 的一条对称轴是
的一条对称轴是![]()
B. 函数![]() 的一个对称中心是
的一个对称中心是![]()
C. 函数![]() 的一条对称轴是
的一条对称轴是![]()
D. 函数![]() 的一个对称中心是
的一个对称中心是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的坐标方程为
的坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切.
相切.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() 、
、![]() 于原点
于原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数为( )
①命题“![]() 中,若
中,若![]() ,则
,则![]() ”的逆命题是真命题
”的逆命题是真命题
②若命题![]() ,则
,则![]()
③“命题![]() 为真命题”是“命题
为真命题”是“命题![]() 为假命题”的充要条件
为假命题”的充要条件
④设![]() 均为非零向量,则“
均为非零向量,则“![]() ”是“
”是“![]() 与
与![]() 的夹角为锐角”的必要不充分条件
的夹角为锐角”的必要不充分条件
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com