【答案】
分析:(1)设椭圆C
1的方程,利用离心率为
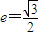
,可得a=2b.由椭圆几何性质知,当P为椭圆的短袖端点时,△PF
1F
2的面积最大,根据△PF
1F
2面积的最大值为
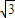
,建立方程,即可求得椭圆C
1的方程;
(2)用坐标表示向量,利用
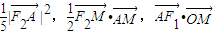
成等差数列,建立方程,整理可得M的轨迹C
2的方程;
(3)l的斜率存在时,设l方程代入椭圆方程,利用韦达定理,借助于坐标表示
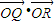
,结合l与C
2相切,可得
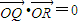
;当l的斜率不存在时,l:x=
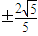
,代入椭圆方程,求出Q,R的坐标,即可证得结论.
解答:(1)解:设椭圆C
1的方程为
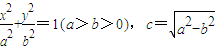
,∴
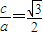
,所以a=2b.
由椭圆几何性质知,当P为椭圆的短袖端点时,△PF
1F
2的面积最大,故
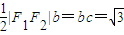
,∴a=2,b=1,
故所求椭圆方程为
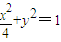
;
(2)解:由(1)知A(0,1),F
1=(
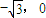
),设M(x,y)则
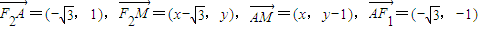
由题意得
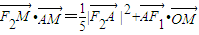
,∴
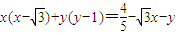
整理得M的轨迹C
2的方程为
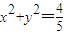
;
(3)证明:l的斜率存在时,设l方程为y=kx+m,代入椭圆方程并整理得(1+4k
2)x
2+8mkx+4m
2-4=0.
△=(8km)
2-16(m
2-1)(1+4k
2)>0,
设Q(x
1,y
1),R(x
2,y
2),∴
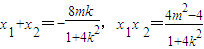
所以
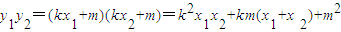
,
则
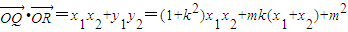
=
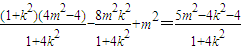
又因为l与C
2相切,所以
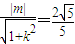
,∴5m
2-4k
2-4=0
所以
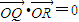
,
当l的斜率不存在时,l:x=
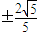
,代入椭圆方程解得
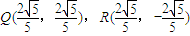
或
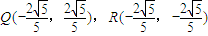
,此时
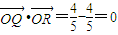
综上所述,
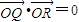 点评:
点评:本题考查椭圆的标准方程,考查向量知识的运用,考查直线与椭圆的位置关系,正确运用韦达定理是关键.

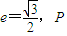 为椭圆上一动点,F1、F2分别为椭圆的左、右焦点,且△PF1F2面积的最大值为
为椭圆上一动点,F1、F2分别为椭圆的左、右焦点,且△PF1F2面积的最大值为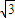 .
.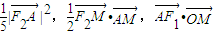 成等差数列,求动点M的轨迹C2的方程;
成等差数列,求动点M的轨迹C2的方程;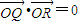 .
.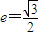 ,可得a=2b.由椭圆几何性质知,当P为椭圆的短袖端点时,△PF1F2的面积最大,根据△PF1F2面积的最大值为
,可得a=2b.由椭圆几何性质知,当P为椭圆的短袖端点时,△PF1F2的面积最大,根据△PF1F2面积的最大值为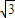 ,建立方程,即可求得椭圆C1的方程;
,建立方程,即可求得椭圆C1的方程;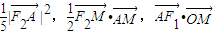 成等差数列,建立方程,整理可得M的轨迹C2的方程;
成等差数列,建立方程,整理可得M的轨迹C2的方程;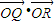 ,结合l与C2相切,可得
,结合l与C2相切,可得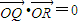 ;当l的斜率不存在时,l:x=
;当l的斜率不存在时,l:x=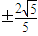 ,代入椭圆方程,求出Q,R的坐标,即可证得结论.
,代入椭圆方程,求出Q,R的坐标,即可证得结论.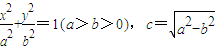 ,∴
,∴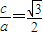 ,所以a=2b.
,所以a=2b.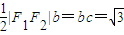 ,∴a=2,b=1,
,∴a=2,b=1,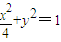 ;
;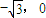 ),设M(x,y)则
),设M(x,y)则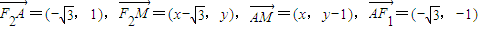
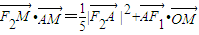 ,∴
,∴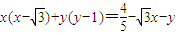
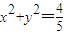 ;
;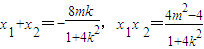
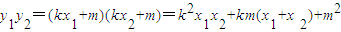 ,
,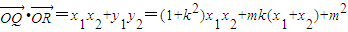 =
=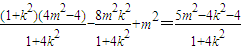
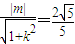 ,∴5m2-4k2-4=0
,∴5m2-4k2-4=0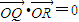 ,
,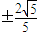 ,代入椭圆方程解得
,代入椭圆方程解得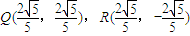 或
或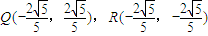 ,此时
,此时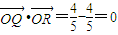
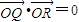


 已知椭圆C1的中心在原点,离心率为
已知椭圆C1的中心在原点,离心率为