
 已知焦点在x轴上的椭圆C过点(0,1),且离心率为
已知焦点在x轴上的椭圆C过点(0,1),且离心率为 ,Q为椭圆C的左顶点.
,Q为椭圆C的左顶点.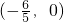 的直线l与椭圆C交于A,B两点.
的直线l与椭圆C交于A,B两点. (a>b>0),且a2=b2+c2.
(a>b>0),且a2=b2+c2. ,可知:b=1,
,可知:b=1, =
= .…(2分)
.…(2分) .…(3分)
.…(3分) .
. ,解得
,解得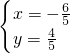
 ,
, ),B(-
),B(- ,-
,- )(不妨设点A在x轴上方).…(5分)
)(不妨设点A在x轴上方).…(5分) .…(6分)
.…(6分) )(k≠0).
)(k≠0).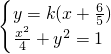 消去y得:(25+100k2)x2+240k2x+144k2-100=0.
消去y得:(25+100k2)x2+240k2x+144k2-100=0. ,0)在椭圆C的内部,显然△>0.
,0)在椭圆C的内部,显然△>0.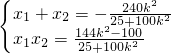 …(8分)
…(8分) =(x1+2,y1),
=(x1+2,y1),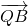 =(x2+2,y2),y1=k(x1+
=(x2+2,y2),y1=k(x1+ ),y2=k(x2+
),y2=k(x2+ ),
), •
•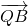 =(x1+2)(x2+2)+y1y2=(1+k2)x1x2+(2+
=(x1+2)(x2+2)+y1y2=(1+k2)x1x2+(2+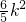 )(x1+x2)+4+
)(x1+x2)+4+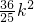
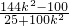 +(2+
+(2+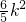 )(
)(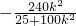 )+4+
)+4+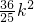 =0
=0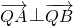 .
.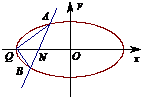 假设存在直线l使得△QAB为等腰三角形,则|QA|=|QB|.
假设存在直线l使得△QAB为等腰三角形,则|QA|=|QB|. ,0)为N.
,0)为N.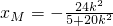 ,
,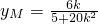 .
.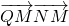 =(
=( )•(
)•(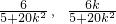 )=
)=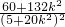 ≠0
≠0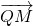 与
与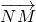 不垂直,矛盾.
不垂直,矛盾. (a>b>0),根据a2=b2+c2,椭圆C过点(0,1),离心率为
(a>b>0),根据a2=b2+c2,椭圆C过点(0,1),离心率为 ,即可求得椭圆C的标准方程;
,即可求得椭圆C的标准方程; ,与椭圆方程联立,求得A,B的坐标,可得直线AQ的斜率、直线BQ的斜率-1,即可求得∠AQB的大小;
,与椭圆方程联立,求得A,B的坐标,可得直线AQ的斜率、直线BQ的斜率-1,即可求得∠AQB的大小; )(k≠0),与椭圆方程联立,利用韦达定理及向量的数量积,可得△QAB为直角三角形,假设存在直线l使得△QAB为等腰三角形,计算
)(k≠0),与椭圆方程联立,利用韦达定理及向量的数量积,可得△QAB为直角三角形,假设存在直线l使得△QAB为等腰三角形,计算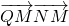 ,即可得到结论.
,即可得到结论.

科目:高中数学 来源: 题型:
| 2m |
| 3 |
| x2 |
| 4m2 |
| y2 |
| 3m2 |
| 2m |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |

| k |
| 2 |
| k |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:中学教材标准学案 数学 高二上册 题型:044
解答题
已知椭圆![]() +
+![]() =1的焦点为F1、F2,能否在x轴下方的椭圆弧上找到一点M,使M到下准线的距离|MN|等于点M到焦点F1、F2的距离的比例中项?若存在,求出M点坐标;若不存在,说明理由.
=1的焦点为F1、F2,能否在x轴下方的椭圆弧上找到一点M,使M到下准线的距离|MN|等于点M到焦点F1、F2的距离的比例中项?若存在,求出M点坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2013年湖南省怀化市高考数学二模试卷(理科)(解析版) 题型:选择题
 的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,
的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,
 ;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点
;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点 对称;⑤函数
对称;⑤函数 时AM过椭圆的右焦点.其中所有的真命题是( )
时AM过椭圆的右焦点.其中所有的真命题是( )查看答案和解析>>
科目:高中数学 来源:2011年上海市浦东新区高考数学三模试卷(理科)(解析版) 题型:解答题
 和椭圆弧
和椭圆弧

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com