解:(Ⅰ)由题设易知f(x)=lnx,g(x)=lnx+

,
∴g′(x)=

,令g′(x)=0,得x=1,
当x∈(0,1)时,g′(x)<0,故g(x)的单调递减区间是(0,1),
当x∈(1,+∞)时,g′(x)>0,故g(x)的单调递增区间是(1,+∞),
因此x=1是g(x)的唯一极值点,且为极小值点,从而是最小值点,
∴最小值为g(1)=1;
(Ⅱ)

=-lnx+x,
设h(x)=g(x)-

=2lnx-x+

,
则h′(x)=
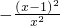
,
当x=1时,h(1)=0,即g(x)=

,
当x∈(0,1)∪(1,+∞)时,h′(x)<0,h′(1)=0,
因此,h(x)在(0,+∞)内单调递减,
当0<x<1,时,h(x)>h(1)=0,即g(x)>

,
当x>1,时,h(x)<h(1)=0,即g(x)<

,
(Ⅲ)满足条件的x
0 不存在.证明如下:证法一 假设存在x
0>0,
使|g(x)-g(x
0)|<

成立,即对任意x>0,
有
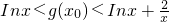
,(*)但对上述x
0,取
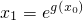
时,
有 Inx
1=g(x
0),这与(*)左边不等式矛盾,
因此,不存在x
0>0,使|g(x)-g(x
0)|<

成立.
证法二 假设存在x
0>0,使|g(x)-g(x
0)|成<

立.
由(Ⅰ)知,
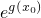
的最小值为g(x)=1.
又
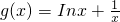
>Inx,
而x>1 时,Inx 的值域为(0,+∞),
∴x≥1 时,g(x) 的值域为[1,+∞),从而可取一个x
1>1,
使 g(x
1)≥g(x
0)+1,即g(x
1)-g(x
0)≥1,
故|g(x
1)-g(x
0)|≥1>

,与假设矛盾.
∴不存在x
0>0,使|g(x)-g(x
0)|<

成立.
分析:(I)根据题意求出f(x)的解析式,代入g(x)=f(x)+f′(x).求出g(x),求导,令导数等于零,解方程,跟据g′(x),g(x)随x的变化情况即可求出函数的单调区间和最小值;
(Ⅱ)构造函数h(x)=g(x)

,利用导数求该函数的最小值,从而求得g(x)与

的大小关系;
(Ⅲ)证法一:假设存在x
0>0,使|g(x)-g(x
0)|<

成立,即对任意x>0,解此绝对值不等式,取
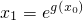
时,得出矛盾;
证法二 假设存在x
0>0,使|g(x)-g(x
0)|成<

立,转化为求函数的值域,得出矛盾.
点评:此题是个难题.考查利用导数研究函数的单调性和在闭区间上的最值问题,对方程f'(x)=0根是否在区间[0,1]内进行讨论,体现了分类讨论的思想方法,增加了题目的难度.其中问题(III)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.

 ,g(x)=f(x)+f′(x).
,g(x)=f(x)+f′(x). 的大小关系;
的大小关系; 对任意x>0成立?若存在,求出x0的取值范围;若不存在请说明理由.
对任意x>0成立?若存在,求出x0的取值范围;若不存在请说明理由. ,
, ,令g′(x)=0,得x=1,
,令g′(x)=0,得x=1, =-lnx+x,
=-lnx+x, =2lnx-x+
=2lnx-x+ ,
,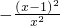 ,
, ,
, ,
, ,
, 成立,即对任意x>0,
成立,即对任意x>0,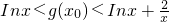 ,(*)但对上述x0,取
,(*)但对上述x0,取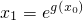 时,
时, 成立.
成立. 立.
立.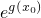 的最小值为g(x)=1.
的最小值为g(x)=1. 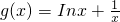 >Inx,
>Inx, ,与假设矛盾.
,与假设矛盾.  成立.
成立. ,利用导数求该函数的最小值,从而求得g(x)与
,利用导数求该函数的最小值,从而求得g(x)与 的大小关系;
的大小关系; 成立,即对任意x>0,解此绝对值不等式,取
成立,即对任意x>0,解此绝对值不等式,取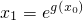 时,得出矛盾;
时,得出矛盾; 立,转化为求函数的值域,得出矛盾.
立,转化为求函数的值域,得出矛盾.
