Question

点P(x，y)在不等式组表示的平面区域内，若点P(x，y)到直线y=kx-1(k>0)的最大距离为2，则k=   ．

 

Answer 1

【答案】

【解析】

试题分析：作出题中不等式组对应的平面区域，得到△ABC及其内部，而直线y=kx-1经过定点（0，-1）是△ABC下方的一点，由此观察图形得到平面区域内的点B（0，3）到直线y=kx-1的距离最大．最后根据点到直线距离公式建立关于k的方程，解之即可得到实数k的值解：作出不等式组表示的平面区域，得到如图所示

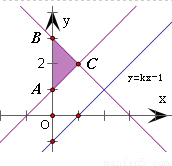
的△ABC及其内部，其中A（0，1），B（0，3），C（1，2）∵直线y=kx-1经过定点（0，-1），∴△ABC必定在直线y=kx-1的上方时，由此结合图形加以观察，得到平面区域内的点B（0，3）到直线y=kx-1的距离最大，将直线y=kx-1化成一般式，得kx-y-1=0因此，可得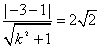 ，解之即可得到k=1,故答案为： 1

考点：线性规划的最优解

点评：本题给出平面区域内点到直线y=kx-1的距离最大值为2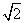 ，求实数k的值，着重考查了点到直线的距离公式和简单线性规划等知识，属于基础题