
过点(1,0)的直线l与中心在原点,焦点在x轴上且离心率为![]() 的椭圆C相交于A、B两点,直线y=
的椭圆C相交于A、B两点,直线y=![]() x过线段AB的中点,同时椭圆C上存在一点与右焦点关于直线l对称,试求直线l与椭圆C的方程.
x过线段AB的中点,同时椭圆C上存在一点与右焦点关于直线l对称,试求直线l与椭圆C的方程.
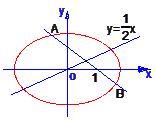
所求椭圆C的方程为![]() =1,l的方程为y=-x+1
=1,l的方程为y=-x+1
解法一: 由e=![]() ,得
,得![]() ,从而a2=2b2,c=b.
,从而a2=2b2,c=b.
设椭圆方程为x2+2y2=2b2,A(x1,y1),B(x2,y2)在椭圆上.
则x12+2y12=2b2,x22+2y22=2b2,两式相减得,(x12-x22)+2(y12-y22)=0,![]()
设AB中点为(x0,y0),则kAB=-![]() ,又(x0,y0)在直线y=
,又(x0,y0)在直线y=![]() x上,y0=
x上,y0=![]() x0,于是-
x0,于是-![]() =-1,kAB=-1,设l的方程为y=-x+1.
=-1,kAB=-1,设l的方程为y=-x+1.
右焦点(b,0)关于l的对称点设为(x′,y′),

由点(1,1-b)在椭圆上,得1+2(1-b)2=2b2,b2=![]() .
.
∴所求椭圆C的方程为![]() =1,l的方程为y=-x+1.
=1,l的方程为y=-x+1.
解法二: 由e=![]() ,从而a2=2b2,c=b.
,从而a2=2b2,c=b.
设椭圆C的方程为x2+2y2=2b2,l的方程为y=k(x-1),
将l的方程代入C的方程,得(1+2k2)x2-4k2x+2k2-2b2=0,则x1+x2=![]() ,y1+y2=k(x1-1)+k(x2-1)=k(x1+x2)-2k=-
,y1+y2=k(x1-1)+k(x2-1)=k(x1+x2)-2k=-![]() .
.
直线l: y=![]() x过AB的中点(
x过AB的中点(![]() ),则
),则![]() ,解得k=0,或k=-1.
,解得k=0,或k=-1.
若k=0,则l的方程为y=0,焦点F(c,0)关于直线l的对称点就是F点本身,不能在椭圆C上,所以k=0舍去,从而k=-1,直线l的方程为y=-(x-1),即y=-x+1,以下同解法一.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:全优设计选修数学-2-1苏教版 苏教版 题型:013
过点(1,0)的直线与双曲线![]() =1的右支交于A、B两点,则直线AB的斜率k的取值范围是
=1的右支交于A、B两点,则直线AB的斜率k的取值范围是
|k|≥1
![]() <|k|<2
<|k|<2
|k|≤![]()
|k|<1
查看答案和解析>>
科目:高中数学 来源:江苏省泰州中学2010-2011学年高二下学期期中考试数学文科试题 题型:022
若存在过点(1,0)的直线与曲线y=x3和y=ax2+![]() x-9都相切,则a等于________.
x-9都相切,则a等于________.
查看答案和解析>>
科目:高中数学 来源:江西省六校2012届高三第一次联考数学理科试题 题型:044
已知定义在(0,+∞)上的函数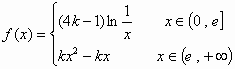 是增函数
是增函数
(1)求常数k的取值范围
(2)过点(1,0)的直线与f(x)(![]() )的图象有交点,求该直线的斜率的取值范围
)的图象有交点,求该直线的斜率的取值范围
查看答案和解析>>
科目:高中数学 来源:2012届湖北省高二下学期期中考试理科数学卷 题型:解答题
过点(1,0)的直线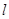 与中心在原点,焦点在x轴上且离心率为
与中心在原点,焦点在x轴上且离心率为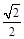 的椭圆C相交于A、B两点,直线y=
的椭圆C相交于A、B两点,直线y=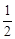 x过线段AB的中点,同时椭圆C上存在一点与其右焦点关于直线l对称,试求直线l与椭圆C的方程
x过线段AB的中点,同时椭圆C上存在一点与其右焦点关于直线l对称,试求直线l与椭圆C的方程
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com