练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本题满分14分）从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同．

    （Ⅰ）若抽取后又放回,抽取3次,求恰好抽到2次为红球的概率;

    （Ⅱ）若抽取后不放回,设抽完红球所需的次数为,求的分布列及期望．

     

    【答案】

    解: （Ⅰ）抽取一次抽到红球的概率为--------------------------------2分

    所以抽取3次恰好抽到2次为红球的概率为-----------4分

    （Ⅱ）-----------------------------------------------------1分

    ,,,

    ．----------------------------------------------4分

    2

    3

    4

    5

    P

    的分布列为                                                      

                                                                                            

     

     

    数学期望．--------------------------3分

     

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2012-2013学年浙江省温州市高三第一次适应性测试理科数学试卷（解析版） 题型：解答题

    （本题满分14分）

    从装有大小相同的2个红球和6个白球的袋子中，每摸出2个球为一次试验，直到摸出的球中有红球（不放回），则试验结束．

    （Ⅰ）求第一次试验恰摸到一个红球和一个白球概率；

    （Ⅱ）记试验次数为，求的分布列及数学期望．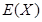

     

    查看答案和解析>>

    科目：高中数学 来源：江苏省淮安市淮阴区2009-2010学年度第二学期期末高一年级调查测试数学试题 题型：解答题

    （本题满分14分）

    从3名男生和2名女生中任选2人参加学校演讲比赛。

    ⑴求所选2人恰有名女生的概率；   

    ⑵求所选2人中至少有名女生的概率．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本题满分14分）

    从3名男生和2名女生中任选2人参加学校演讲比赛。

    ⑴求所选2人恰有名女生的概率；   

    ⑵求所选2人中至少有名女生的概率．

     

                                                                              

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本题满分14分）

    从3名男生和2名女生中任选2人参加学校演讲比赛。

    ⑴求所选2人恰有名女生的概率；   

    ⑵求所选2人中至少有名女生的概率．

     

                                                                              

    查看答案和解析>>

    同步练习册答案