
函数f(x)=sin xcos x+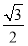 cos 2x的最小正周期T=________,振幅A=________.
cos 2x的最小正周期T=________,振幅A=________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(解析版) 题型:解答题
已知四边形ABCD是菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,G,H分别是CE,CF的中点.

(1)求证:平面AEF∥平面BDGH
(2)若平面BDGH与平面ABCD所成的角为60°,求直线CF与平面BDGH所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-4-2练习卷(解析版) 题型:选择题
已知数列{an}的通项公式是an= ,若前n项和为10,则项数n为( ).
,若前n项和为10,则项数n为( ).
A.11 B.99 C.120 D.121
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-3-2练习卷(解析版) 题型:填空题
已知△ABC的三边长成公比为 的等比数列,则其最大角的余弦值为________.
的等比数列,则其最大角的余弦值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-3-1练习卷(解析版) 题型:解答题
设函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,-π<φ≤π)在x= 处取得最大值2,其图象与x轴的相邻两个交点的距离为
处取得最大值2,其图象与x轴的相邻两个交点的距离为 .
.
(1)求f(x)的解析式;
(2)求函数g(x)= 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(解析版) 题型:解答题
已知函数f(x)=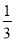 x3+
x3+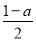 x2-ax-a,x∈R,其中a>0.
x2-ax-a,x∈R,其中a>0.
(1)求函数f(x)的单调区间;
(2)若函数f(x)在区间(-2,0)内恰有两个零点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(解析版) 题型:选择题
设函数f(x)=ax2+bx+c(a,b,c∈R),若x=-1为函数f(x)ex的一个极值点,则下列图象不可能为y=f(x)的图象是( ).

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-1练习卷(解析版) 题型:解答题
已知奇函数f(x)在定义域[-2,2]上单调递减,求满足f(1-m)+f(1-m2)<0的实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习1-1集合等练习卷(解析版) 题型:解答题
已知二次函数f(x)=ax2+x,若对任意x1、x2∈R,恒有2f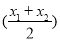 ≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.
≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.
(1)求集合A;
(2)设集合B={x||x+4|<a},若集合B是集合A的子集,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com