
如图,A,B是海面上位于东西方向相距 海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距
海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距 海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
需要1小时
解析试题分析:由题意知AB= 海里,∠DBA=90°-60°=30°,∠DAB=45°,∴∠ADB=105°。
海里,∠DBA=90°-60°=30°,∠DAB=45°,∴∠ADB=105°。
在△DAB中,由正弦定理得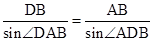 ,∴DB=
,∴DB=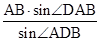 =
=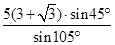
= =
= (海里),
(海里),
又∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°,BC= 海里,
海里,
在△DBC中,由余弦定理得
CD2=BD2+BC2-2BD•BC•cos∠DBC=300+1200-2×10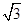 ×20
×20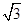 ×
× =900,
=900,
∴CD=30(海里),则需要的时间t==1(小时).
答:救援船到达D点需要1小时.
考点:正弦定理、余弦定理的应用。
点评:典型题,本题综合考查正弦定理、余弦定理的应用,本题解答结合图形,在不同的几个三角形中,灵活运用正弦定理或余弦定理,反映应用数学知识的灵活性。解决“追击问题”,准确找出题中的方向角是解题的关键之一。


科目:高中数学 来源: 题型:解答题
如图,甲船以每小时 海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西 的方向
的方向 处,此时两船相距20海里.当甲船航行20分钟到达
处,此时两船相距20海里.当甲船航行20分钟到达 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com