
分析 (1)由奇函数的定义,结合对数的运算性质,可得a=-1;
(2)运用单调性的定义,结合对数函数的单调性即可得证;
(3)由题意可得即f(x)-($\frac{1}{2}$)x>m恒成立.令g(x)=f(x)-($\frac{1}{2}$)x.只需g(x)min>m,由g(x)的单调性即可得到最小值.
解答 解:(1)由f(x)是奇函数,即为f(-x)=-f(x),
则$lo{g}_{\frac{1}{2}}\frac{1+ax}{-x-1}$=-log${\;}_{\frac{1}{2}}$$\frac{1-ax}{x-1}$,即有$\frac{1+ax}{-x-1}$=$\frac{x-1}{1-ax}$>0,
即有1-a2x2=1-x2,解得a=±1,
检验a=1(舍),故a=-1.
(2)由(1)知f(x)=$lo{g}_{\frac{1}{2}}$($\frac{x+1}{x-1}$),
证明:任取1<m<n,n-1>m-1>0,即有0<$\frac{2}{n-1}$<$\frac{2}{m-1}$,
即1+$\frac{2}{n-1}$<1+$\frac{2}{m-1}$,即0<$\frac{n+1}{n-1}$<$\frac{m+1}{m-1}$,
即有$lo{g}_{\frac{1}{2}}$$\frac{n+1}{n-1}$>$lo{g}_{\frac{1}{2}}$$\frac{m+1}{m-1}$,
即f(n)>f(m),f(x)在(1,+∞)内单调递增.
(3)对于[2,5]上的每一个x的值,不等式f(x)>($\frac{1}{2}$)x+m恒成立,
即f(x)-($\frac{1}{2}$)x>m恒成立.
令g(x)=f(x)-($\frac{1}{2}$)x.只需g(x)min>m,
又易知g(x)在[2,5]上是增函数,
∴g(x)min=g(2)=$lo{g}_{\frac{1}{2}}$3-$\frac{1}{4}$,
则当m<$lo{g}_{\frac{1}{2}}$3-$\frac{1}{4}$时原式恒成立.
点评 本题考查函数的性质和运用,考查不等式恒成立问题的解法,注意运用参数分离和函数的单调性,属于中档题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x-1}$ | B. | y=ln(x-1) | C. | y=ex-1 | D. | y=|tanx| |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
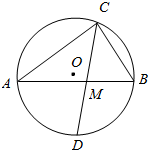 如图,已知AB是⊙O的直径,C为圆上一点,连接CB、AC,点D是半圆弧AB的中点,若圆的半径为4,DC交AB于M点,则DM•DC的范围是32.
如图,已知AB是⊙O的直径,C为圆上一点,连接CB、AC,点D是半圆弧AB的中点,若圆的半径为4,DC交AB于M点,则DM•DC的范围是32.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | (0,1) | C. | [1,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=$\left\{\begin{array}{l}{6,n=1}\\{2×{3}^{n-1},n≥2}\end{array}\right.$ | B. | an=2×3n-1 | ||
| C. | an=2×3n-1+2 | D. | an=$\left\{\begin{array}{l}{6,n=1}\\{2×{3}^{n-1}+2,n≥2}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com