
(1)己知z=x+yi(x,y∈R)满足|z-4i|-|z+2|=0,求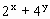 的最小值.
的最小值.
(2)设复数z满足2|z-3-3i|-|z|=0,试求|z|的最大值和最小值.
|
解:(1)由已知条件得 (2)解法1:设z=x+yi(x,y∈R),得2|x+yi-3-3i|-|x+yi|=0, 解法2:设z=r(cosθ+isinθ),代入已知条件并化简得 解法3:将解法1中的方程 解法4:由已知得|z-(3+3i)|= |
|
注 本题的四种解法从不同的侧面反映了求复数模的极值的常用方法:不等式法、三角法、几何法、公式法,它们的共同之处是把复数问题化归为实数问题来解. |


科目:高中数学 来源:高二数学 教学与测试 题型:047
己知(b-c)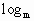 x+(c-a)
x+(c-a)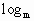 y+(a-b)
y+(a-b)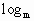 z=0,
z=0,
(1)设a,b,c依次成等差数列,且公差不为0,求证:x,y,z成等比数列;
(2)设正数x,y,z依次成等比数列,且公比不为1,求证:a,b,c成等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com