Question

【题目】设函数

（1）若在点处的切线斜率为，求的值；

（2）求函数的单调区间；

（3）若，求证：在时， .

Answer 1

【答案】（1）；（2）当时， 的单调减区间为.单调增区间为；

当时， 的单调减区间为；（3）证明见解析.

【解析】试题分析：（1）先求出，通过在点处的切线斜率，可得，解得；（2）由（1）知： ，结合导数分①、②两种情况讨论分别令求得 的范围，可得函数增区间， 求得 的范围，可得函数的减区间；；（3）通过变形，只需证明即可，利用，根据指数函数及幂函数的性质、函数的单调性及零点判定定理即得到结论.

试题解析：（1）若在点处的切线斜率为，

，

得.

（2）由

当时，令解得：

当变化时， 随变化情况如表：

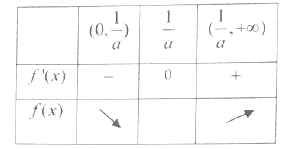
由表可知： 在上是单调减函数，在上是单调增函数

当时， ， 的单调减区间为

所以，当时， 的单调减区间为.单调增区间为

当时， 的单调减区间为

（3）当时，要证，即证

令，只需证

∵

由指数函数及幕函数的性质知： 在上是增函数

∵，∴在内存在唯一的零点，

也即在上有唯一零点

设的零点为，则，即，

由的单调性知：

当时， ， 为减函数

当时， ， 为增函数，

所以当时.

∴.