
已知两点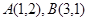 到直线
到直线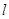 的距离分别为
的距离分别为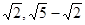 ,则满足条件的直线
,则满足条件的直线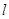 共有( )条
共有( )条
A.1 B.2 C.3 D.4
C
【解析】
试题分析:由A和B的坐标,利用两点间的距离公式求出|AB|的长,然后以A为圆心,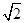 为半径画圆A,以B为圆心
为半径画圆A,以B为圆心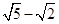 为半径画圆B,由d=R+r,得到两圆外切,可得出公切线有3条,即可得到满足题意的直线l共有3条。
为半径画圆B,由d=R+r,得到两圆外切,可得出公切线有3条,即可得到满足题意的直线l共有3条。
解:∵A(1,2),B(3,1),∴|AB|=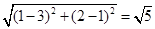 ,分别以A,B为圆心,
,分别以A,B为圆心,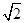 ,
,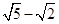 为半径作两个圆,如图所示:
为半径作两个圆,如图所示:
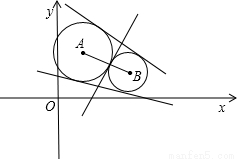
即d=R+r,∴两圆外切,有三条共切线,则满足条件的直线l共有3条.故选C
考点:圆与圆位置关系的判定
点评:此题考查了圆与圆位置关系的判定,以及直线与圆的位置关系,圆与圆位置关系由R,r及d间的关系来判定,当d<R-r时,两圆内含;当d=R-r时,两圆内切;当R-r<d<R+r时,两圆相交;当d=R+r时,两圆外切;当d>R-r时,两圆外离,解题的关键是根据题意画出相应的图形,找出两圆的公切线的条数即为所求直线l的条数


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源:2014届山东省济宁市高二5月质量检测理科数学试卷(解析版) 题型:解答题
定义:设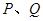 分别为曲线
分别为曲线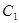 和
和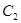 上的点,把
上的点,把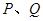 两点距离的最小值称为曲线
两点距离的最小值称为曲线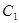 到
到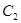 的距离.
的距离.
(1)求曲线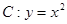 到直线
到直线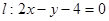 的距离;
的距离;
(2)已知曲线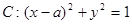 到直线
到直线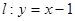 的距离为
的距离为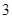 ,求实数
,求实数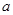 的值;
的值;
(3)求圆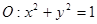 到曲线
到曲线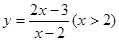 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年大纲版高三上学期单元测试(8)数学试卷 题型:选择题
设双曲线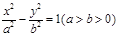 的半焦距为
的半焦距为 ,直线
,直线 过
过 两点.已知原点到
两点.已知原点到
直线 的距离为
的距离为 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.2
B.2或 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2011年天津市南开大学附属中学高考数学模拟试卷(理科)(解析版) 题型:解答题
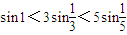
 ”的否定是:“?x∈R,均有ex≥0”;
”的否定是:“?x∈R,均有ex≥0”;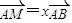 ,
,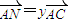 ,则
,则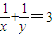 ;
;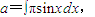 点
点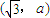 到直线
到直线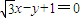 的距离为1;
的距离为1;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com