
如图,在棱长为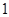 的正方体
的正方体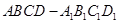 中,
中,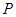 为线段
为线段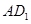 上的点,且满足
上的点,且满足
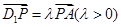 .
.
(Ⅰ)当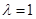 时,求证:平面
时,求证:平面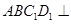 平面
平面 ;
;
(Ⅱ)试证无论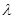 为何值,三棱锥
为何值,三棱锥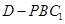 的体积
的体积
恒为定值;
(Ⅲ)求异面直线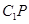 与
与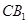 所成的角的余弦值.
所成的角的余弦值.
 18.解:
18.解:
方法一、证明:(Ⅰ)∵正方体 中,
中,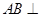 面
面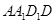 ,
,
又 ∴平面
∴平面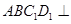 平面
平面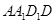 , ………………2分
, ………………2分
∵ 时,
时,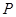 为
为 的中点,∴
的中点,∴ ,
,
又∵平面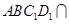 平面
平面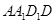
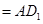 ,
,
∴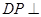 平面
平面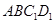 ,
,
又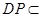 平面
平面 ,∴平面
,∴平面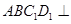 平面
平面 .………4分
.………4分
(Ⅱ)∵ ,
, 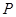 为线段
为线段 上的点,
上的点,
∴三角形 的面积为定值,即
的面积为定值,即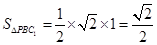 ,
,
………………6分
又∵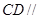 平面
平面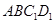 ,∴点
,∴点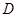 到平面
到平面 的距离为定值,即
的距离为定值,即 , ………………8分
, ………………8分
∴三棱锥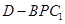 的体积为定值,即
的体积为定值,即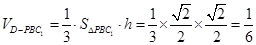 .
.
也即无论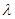 为何值,三棱锥
为何值,三棱锥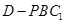 的体积恒为定值
的体积恒为定值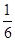 ;………………………10分
;………………………10分
(Ⅲ)∵由(Ⅰ)易知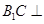 平面
平面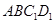 ,
,
又 平面
平面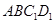 ,∴
,∴ ,
…………………………12分
,
…………………………12分
 即异面直线
即异面直线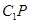 与
与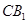 所成的角为定值
所成的角为定值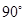 ,从而其余弦值为
,从而其余弦值为 .…………………13分
.…………………13分
方法二、如图,以点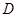 为坐标原点,建立如图所示的坐标系.
为坐标原点,建立如图所示的坐标系.
(Ⅰ)当 时,即点
时,即点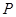 为线段
为线段 的中点,则
的中点,则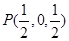 ,又
,又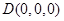 、
、
∴ ,
,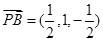 ,设平面
,设平面 的法向量为
的法向量为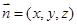 ,……1分
,……1分
则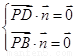 ,即
,即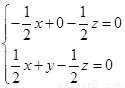 ,令
,令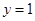 ,解得
,解得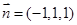 ,
…2分
,
…2分
又∵点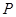 为线段
为线段 的中点,∴
的中点,∴ ,∴
,∴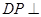 平面
平面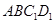 ,
,
∴平面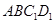 的法向量为
的法向量为 ,
……………3分
,
……………3分
∵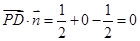 ,
,
∴平面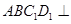 平面
平面 ,
………………………4分
,
………………………4分
(Ⅱ)略;
(Ⅲ)∵ ,∴
,∴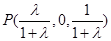 , …………………10分
, …………………10分
又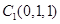 、
、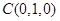 、
、 ,
,
∴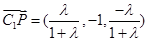 ,
, , ……………………………11分
, ……………………………11分
∵ …………………………………12分
…………………………………12分
∴不管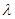 取值多少,都有
取值多少,都有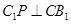 ,即异面直线
,即异面直线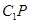 与
与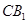 所成的角的余弦值为0.……13分
所成的角的余弦值为0.……13分
【解析】略


科目:高中数学 来源: 题型:
 (2013•泉州模拟)如图,在棱长为1的正方体ABCD-A1B1C1D1的对角线AC1上任取一点P,以A为球心,AP为半径作一个球.设AP=x,记该球面与正方体表面的交线的长度和为f(x),则函数f(x)的图象最有可能的是( )
(2013•泉州模拟)如图,在棱长为1的正方体ABCD-A1B1C1D1的对角线AC1上任取一点P,以A为球心,AP为半径作一个球.设AP=x,记该球面与正方体表面的交线的长度和为f(x),则函数f(x)的图象最有可能的是( )查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省泉州市毕业班(第二轮)质量检测文科数学试卷(解析版) 题型:选择题
如图,在棱长为1的正方体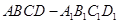 的对角线
的对角线 上任取一点P,以
上任取一点P,以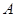 为球心,
为球心, 为半径作一个球.设
为半径作一个球.设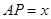 ,记该球面与正方体表面的交线的长度和为
,记该球面与正方体表面的交线的长度和为 ,则函数
,则函数 的图象最有可能的是( )
的图象最有可能的是( )
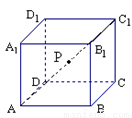

A. B. C. D.
查看答案和解析>>
科目:高中数学 来源:2010年湖北省高三第三次模拟考试(理科)数学卷 题型:选择题
如图,在棱长为2的正方体 内有一个内切球O,则过棱
内有一个内切球O,则过棱 和
和 的中点
的中点 、
、 的直线与球面交点为
的直线与球面交点为 、
、 ,则
,则 、
、 两点间的球面距离为( )
两点间的球面距离为( )
 A.
A. B.
B. C.
C. D.
D. 
查看答案和解析>>
科目:高中数学 来源:湖北省黄冈中学2010年高三年级第二次模拟考试(理) 题型:选择题
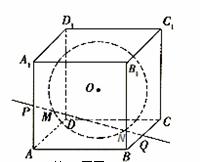 如图,在棱长为2的正方体
如图,在棱长为2的正方体 内有一个内切球O,则过棱
内有一个内切球O,则过棱 和
和 的中点
的中点 、
、 的直线与球面交点为
的直线与球面交点为 、
、 ,则
,则 、
、 两点间的球面距离为 ( )
两点间的球面距离为 ( )
A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com