
| OA |
| OB |
| OC |
| OA |
| 3 |
| OB |
| 1 |
| 2 |
| OC |
| 0 |
| 1 |
| 2 |
| π |
| 3 |
| 7π |
| 12 |
| 2 |
| π |
| 2 |
| 3 |
| 1 |
| 2 |
| 3π |
| 2 |
| 3π |
| 2 |
| OA |
| 3 |
| OB |
| 1 |
| 2 |
| OC |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| 7π |
| 2 |
| 7π |
| 2 |
| x1+x2 |
| 2 |
| x2+x3 |
| 2 |
| 3π |
| 2 |
| 3π |
| 2 |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 2 |
| 2 |
| π |
| 6 |
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 7 |
| 2 |


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年安徽信息交流文)设A、B、C是直线l上的三个不同的点,点![]() 是坐标原点,如果
是坐标原点,如果![]() ,那么点(x,y)的轨迹是( )
,那么点(x,y)的轨迹是( )
A.圆 B.椭圆 C.双曲线 D.抛物线
查看答案和解析>>
科目:高中数学 来源:2008-2009学年四川省资阳市高一(下)期末数学试卷(解析版) 题型:解答题
 满足关系:
满足关系: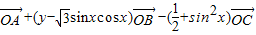 =
=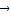 .
.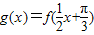 ,
,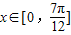 的图象与直线y=b的交点的横坐标成等差数列,试求实数b的值;
的图象与直线y=b的交点的横坐标成等差数列,试求实数b的值;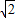 (sinx+cosx)+sin2x-a,若对任意的
(sinx+cosx)+sin2x-a,若对任意的 ,不等式h(x1)≤f(x2)恒成立,求实数a的取值范围.
,不等式h(x1)≤f(x2)恒成立,求实数a的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| OA |
| OB |
| OC |
| OA |
| 3 |
| OB |
| 1 |
| 2 |
| OC |
| 0 |
| 1 |
| 2 |
| π |
| 3 |
| 7π |
| 12 |
| 2 |
| π |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com