
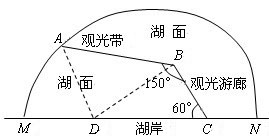
根据长沙市建设大河西的规划,市旅游局拟在咸嘉湖建立西湖生态文化公园。如图,设计方案中利用湖中半岛上建一条长为![]()
![]() 的观光带AB,同时建一条连接观光带和湖岸的长为2
的观光带AB,同时建一条连接观光带和湖岸的长为2![]() 的观光游廊BC,且BC与湖岸MN(湖岸可看作是直线)的夹角为60°,BA与BC的夹角为150°,并在湖岸上的D处建一个观光亭,设CD=xkm(1<x<4)。
的观光游廊BC,且BC与湖岸MN(湖岸可看作是直线)的夹角为60°,BA与BC的夹角为150°,并在湖岸上的D处建一个观光亭,设CD=xkm(1<x<4)。
(Ⅰ)用x分别表示tan∠BDC和tan∠ADM;
(Ⅱ)试确定观光亭D的位置,使得在观光亭D处观赏观光带AB的视觉效果最佳。
(Ⅰ)![]() ,
,![]()
(Ⅱ)
(Ⅰ)设湖岸线为l,过点A、B分别作![]() 的垂线,垂足为E、F,延长AB交
的垂线,垂足为E、F,延长AB交![]() 于点G。
于点G。

因为BC=2,∠BCF=60°,则![]() ,
,![]() ,
,
因为CD=x>1,则DF=CD-CF=x-1,
所以![]() 。 (3分)
。 (3分)
因为∠ABC=150°,则∠CBG=30°,又∠BCF=60°,
则∠BGC=30°,所以![]() 。
。
因为AB=![]() ,则AG=AB+BG=
,则AG=AB+BG=![]() ,
,
所以AE=AGsin30°=![]() ,GE=AGcos30°=6。
,GE=AGcos30°=6。
又GC=BC=2,则CE=GE-GC=4,因为CD=x<4,则DE=CE-CD=4-x,
所以![]() 。 (7分)
。 (7分)
(Ⅱ)设∠ADB=θ,则
![]()

![]() (
(![]() )。 (9分)
)。 (9分)
令x+2=t,则 。
。
因为![]() ,则
,则![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时取等号.所以当
时取等号.所以当![]() ,即
,即![]() 时,tanθ取最大值。
时,tanθ取最大值。
又θ为锐角,则当![]() 时θ取最大值。 (12分)
时θ取最大值。 (12分)
故当观光亭D建在距离C点![]() 时,在D处观赏观光带AB的视觉效果最佳。(13分)
时,在D处观赏观光带AB的视觉效果最佳。(13分)


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
(本小题满分13分) 根据长沙市建设大河西的规划,市旅游局拟在咸嘉湖建立西湖生态文化公园. 如图,设计方案中利用湖中半岛上建一条长为![]()
![]() 的观光带AB,同时建一条连接观光带和湖岸的长为2
的观光带AB,同时建一条连接观光带和湖岸的长为2![]() 的观光游廊BC,且BC与湖岸MN(湖岸可看作是直线)的夹角为60°,BA与BC的夹角为150°,并在湖岸上的D处建一个观光亭,设CD=xkm(1<x<4).
的观光游廊BC,且BC与湖岸MN(湖岸可看作是直线)的夹角为60°,BA与BC的夹角为150°,并在湖岸上的D处建一个观光亭,设CD=xkm(1<x<4).
 (Ⅰ)用x分别表示tan∠BDC和tan∠ADM;
(Ⅰ)用x分别表示tan∠BDC和tan∠ADM;
(Ⅱ)试确定观光亭D的位置,使得在观光亭D处观赏
观光带AB的视觉效果最佳.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com