分析:(1)由题设形式可以看出,题设中给出了关于数列an的面的一个方程,即一个递推关系,所以应该对此递推关系进行变形整理以发现其中所蕴含的规律,观察发现若对方程两边取倒数则可以得到一个类似等差数列的形式,对其中参数进行讨论,分类求其通项即可.
(2)由于本题中条件较少,解题思路不宜用综合法直接分析出,故求解本题可以采取分析法的思路,由结论探究其成立的条件,再证明此条件成立,即可达到证明不等式的目的.
解答:解:(1)∵
an =(n≥2),
∴
=+×(n≥2),
当b=1时,
=1+(n≥2),
∴数列{
}是以
为首项,以1为公差的等差数列,
∴
=1+(n-1)×1=n,即a
n=1,
当b>0,且b≠1时,
+=(+)(n≥2),
即数列{
+}是以
+=
为首项,公比为
的等比数列,
∴
+=
×
()n-1=
,即a
n=
,
∴数列{a
n}的通项公式是
an=(2)证明:当b=1时,不等式显然成立
当b>0,且b≠1时,a
n=
,要证对于一切正整数n,2a
n≤b
n+1+1,只需证2×
≤b
n+1+1,即证
2nbn≤(bn+1+1)×∵
(bn+1+1)×=
(bn+1+1)×=(b
n+1+1)×(b
n-1+b
n-2+…+b+1)
=(b
2n+b
2n-1+…+b
n+2+b
n+1)+(b
n-1+b
n-2+…+b+1)
=b
n[(b
n+b
n-1+…+b
2+b)+(
+
+…+
+)]
≥b
n(2+2+…+2)=2nb
n所以不等式成立,
综上所述,对于一切正整数n,有2a
n≤b
n+1+1,
点评:本题考点是数列的递推式,考查根据数列的递推公式求数列的通项,研究数列的性质的能力,本题中递推关系的形式适合用取倒数法将所给的递推关系转化为有规律的形式,两边取倒数,条件许可的情况下,使用此技巧可以使得解题思路呈现出来.数列中有请多成熟的规律,做题时要注意积累这些小技巧,在合适的情况下利用相关的技巧,可以简化做题.在(2)的证明中,采取了分析法的来探究解题的思路,通过本题希望能进一步熟悉分析法证明问题的技巧.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案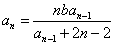 (n≥2)。
(n≥2)。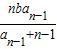 (n≥2)
(n≥2)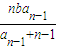 (n≥2)
(n≥2)