已知f(x)=ax2+x-a,a∈R.
(1)若不等式f(x)>(a-1)x2+(2a+1)x-3a-1对任意实数x∈[-1,1]恒成立,求实数a的取值范围;
(2)若a<0,解不等式f(x)>1.
解:(1)原不等式等价于x
2-2ax+2a+1>0对任意的实数x∈[-1,1]恒成立,
设g(x)=x
2-2ax+2a+1=(x-a)
2-a
2+2a+1
①当a<-1时,g
min(x)=g(-1)=1+2a+2a+1>0,得a∈Φ;
②当-1≤a≤1时,
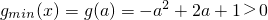
,得

;
③当a>1时,g
min(x)=g(1)=1-2a+2a+1>0,得a>1;
综上
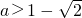
(3)不等式f(x)>1即为ax
2+x-a-1>0,即(x-1)(ax+a+1)>0
因为a<0,所以

,因为
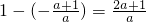
所以当
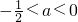
时,
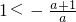
,解集为{x|
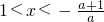
};
当

时,(x-1)
2<0,解集为?;
当
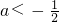
时,
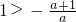
,解集为{x|
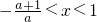
}
分析:(1)原不等式等价于x
2-2ax+2a+1>0对任意的实数x∈[-1,1]恒成立,设g(x)=x
2-2ax+2a+1=(x-a)
2-a
2+2a+1,只需g
min(x)>0即可.
(2)不等式f(x)>1即为ax
2+x-a-1>0,即(x-1)(ax+a+1)>0转化为二次不等式求解,注意分类讨论.
点评:本题考查二次函数性质和一元二次不等式的解法,分类讨论思想,均属基本知识和能力.

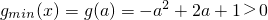 ,得
,得 ;
;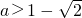
 ,因为
,因为 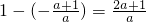
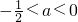 时,
时,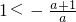 ,解集为{x|
,解集为{x|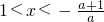 };
}; 时,(x-1)2<0,解集为?;
时,(x-1)2<0,解集为?;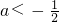 时,
时,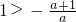 ,解集为{x|
,解集为{x|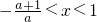 }
}

 名校课堂系列答案
名校课堂系列答案