
分析 可求出$|\overrightarrow{a}|=\sqrt{2}$,并且$\overrightarrow{a},\overrightarrow{b}$夹角已知,从而根据$\overrightarrow{a}•\overrightarrow{b}=\sqrt{2}$即可求出$|\overrightarrow{b}|$的值.
解答 解:$|\overrightarrow{a}|=\sqrt{2}$,$<\overrightarrow{a},\overrightarrow{b}>=\frac{π}{3}$;
∴$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos\frac{π}{3}$
=$\frac{\sqrt{2}}{2}|\overrightarrow{b}|$
=$\sqrt{2}$;
∴$|\overrightarrow{b}|=2$.
故答案为:2.
点评 考查根据向量坐标求向量长度的方法,以及向量数量积的计算公式.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{3}-\sqrt{6}}}{2}$ | B. | $\sqrt{2}-1$ | C. | $\frac{{\sqrt{6}-\sqrt{3}}}{2}$ | D. | $\sqrt{6}-\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
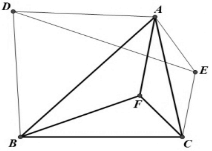 已知,△ABC内有一点F,分别以AB、AC为底边向外作等腰三角形DAB、AEC,且∠BAD=∠BCF,∠ACE=∠CBF.求证:DE平分AF.
已知,△ABC内有一点F,分别以AB、AC为底边向外作等腰三角形DAB、AEC,且∠BAD=∠BCF,∠ACE=∠CBF.求证:DE平分AF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com