Question

如果x⁹+x¹⁰=a+a₁（1+x）+a₂（1+x）²+…+a₉（1+x）⁹+a₁₀（1+x）¹⁰，则a₉=    ．

Answer 1

【答案】分析：把x⁹+x¹⁰ 化为-（1+x）[1-（1+x）]⁹，利用二项式定理展开，即可求得（1+x）⁹的系数a₉的值．
解答：解：由于x⁹+x¹⁰=x⁹•（1+x）=（1+x）•[（1+x）-1]⁹=-（1+x）[1-（1+x）]⁹ 
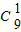
=-（1+x）[1-（1+x）+•（1+x）²-+…+-]，
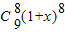
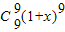
故a₉=-1×+（-1）•（-）=-8，
故答案为-8．
点评：本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，分析所给代数式的特点，把x⁹+x¹⁰ 化为-（1+x）[1-（1+x）]⁹，是解题的关键，属于中档题．