
 ;②y=
;②y=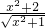 ;③y=log2x+logx2(x>0且x≠1);④y=3x+3-x;⑤
;③y=log2x+logx2(x>0且x≠1);④y=3x+3-x;⑤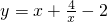 ;⑥
;⑥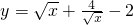 ;⑦y=log2x2+2最小值为2的函数是________(只填序号)
;⑦y=log2x2+2最小值为2的函数是________(只填序号) =|x|+|
=|x|+| |,由基本不等式可判断真假;
|,由基本不等式可判断真假;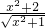 =
= +
+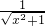 ,由基本不等式可判断真假;
,由基本不等式可判断真假;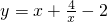 ≤-6可判断真假;
≤-6可判断真假;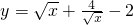 ,由基本不等式可判断真假;
,由基本不等式可判断真假; 同号,故
同号,故 =|x|+|
=|x|+| |,由|x|>0,|
|,由|x|>0,| |>0
|>0 =|x|+|
=|x|+| |≥2
|≥2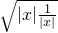 =≥2,故正确;
=≥2,故正确;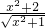 =
= +
+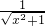 ,由
,由 >0,
>0,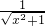 >0,
>0, +
+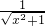 ≥2
≥2 =2,故正确;
=2,故正确;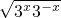 =2,故正确;
=2,故正确;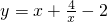 ≤-6,故错误;
≤-6,故错误; >0,
>0, >0,
>0,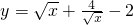 ≥
≥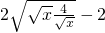 =2,故正确;
=2,故正确;

科目:高中数学 来源:湖南省期末题 题型:填空题
 ;②
;②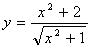 ;③y=log2x+logx2(x>0,且x≠1);
;③y=log2x+logx2(x>0,且x≠1);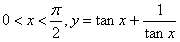 ;⑤y=3x+3-x;⑥
;⑤y=3x+3-x;⑥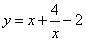 ;⑦
;⑦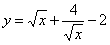 ;
;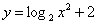 ;其中最小值为2的函数是( )。(填入正确的命题序号)
;其中最小值为2的函数是( )。(填入正确的命题序号) 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com