分析:(1)设中点P的坐标,建立关于点P的方程,从而确定轨迹方程.
(2)利用代入法求点点Q的轨迹.
解答:解:(1)圆C的方程为(x-3)
2+(y-2)
2=4,其圆心为C(3,2),半径为2.
又M∈{M|PC⊥MP,P在已知圆内},
设P点坐标(x,y),则CP的斜率为
(x≠3),MP的斜率为
(x≠-6),
所以
•=-1,化简得x
2+y
2+3x-2y-18=0.
点C(3,2)应在轨迹上,而x=3时,y=2满足方程x
2+y
2+3x-2y-18=0,
所以点P的轨迹是圆x
2+y
2+3x-2y-18=0在已知圆内的一段弧.
(2)设A(x
1,y
1),B(x
2,y
2),Q(x,y),直线AB的斜率为k,则有
MA=(x1+6), MB=(x2+6),MQ=(x+6),
代入
+=,有
+=,
即
=,①
把y=k(x+6)代入x
2+y
2-6x-4y+9=0,得(k
2+1)x
2+2(6k
2-2k-3)x+3(12k
2-8k+3)=0,
x1+x2=-,x1•x2=,②
②代入①并化简得
=⇒2k(x+6)+9x-27=0,而
k=,从而有9x+2y-27=0,所以点Q的轨迹是直线9x+2y-27=0的圆内部分.
点评:本题考查直线与圆的位置关系,考查轨迹方程,运算量较大,综合性较强.

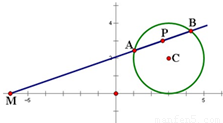
 如图所示,过点M(-6,0)作圆C:x2+y2-6x-4y+9=0的割线,交圆C于A、B两点.
如图所示,过点M(-6,0)作圆C:x2+y2-6x-4y+9=0的割线,交圆C于A、B两点.

 (本小题满分14分)设b>0,椭圆方程为
(本小题满分14分)设b>0,椭圆方程为![]() ,抛物线方程为
,抛物线方程为![]() 。如图所示,过点F(0,b + 2)作x轴的平行线,与抛物线在第一象限的交点为G。已知抛物线在点G的切线经过椭圆的右焦点F1。
。如图所示,过点F(0,b + 2)作x轴的平行线,与抛物线在第一象限的交点为G。已知抛物线在点G的切线经过椭圆的右焦点F1。![]() 所在的直线截椭圆的右下区域为D,
所在的直线截椭圆的右下区域为D,![]() 与区域D有公共点,求m的最小值。
与区域D有公共点,求m的最小值。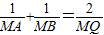 ,求点Q的轨迹.
,求点Q的轨迹.