某学校为高二年级开展第二外语选修课,要求每位同学最多可以选报两门课程.已知有75%的同学选报法语课,有60%的同学选报日语课.假设每个人对课程的选报是相互独立的,且各人的选报相互之间没有影响.
(1)任选1名同学,求其选报过第二外语的概率;
(2)理科:任选3名同学,记ξ为3人中选报过第二外语的人数,求ξ的分布列、期望和方差.
文科:任选3名同学,求3人中恰有1人选报过第二外语的概率.
解:设事件A:选报法语课;事件B:选报日语课.
由题设知,事件A与B相互独立,且P(A)=0.75.P(B)=0.6
(1)解法一:任选1名同学,
该人一门课程均没选报的概率是
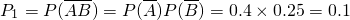
所以该人选报过第二外语的概率是P
2=1-P
1=1-0.1=0.9.…(6分)
解法二:任选1名同学,该人只选报一门课程的概率是

该人选报两门课程的概率是P
4=P(A•B)=0.75×0.6=0.45.
所以该人选报过第二外语的
概率是P
5=P
3+P
4=0.45+0.45=0.9…(6分)
(2)【理科】因为每个人的选报是相互独立的,
所以3人中选报过第二外语的人数ξ服从二项分布B(3,0.9),
P(ξ=k)=C
3k×0.9
k×0.1
3-k,k=0,1,2,3,
即ξ的分布列是
| ξ | 0 | 1 | 2 | 3 |
| P | 0.001 | 0.027 | 0.243 | 0.729 |
…(9分)ξ的期望是Eξ=1×0.027+2×0.243+3×0.729=2.7
(或ξ的期望是Eξ=3×0.9=2.7)…(11分)
ξ的方差是Dξ=3×0.98×(1-0.98)=0.0588…(12分)
【文科】3人中有1人选报过第二外语的概率为C
31×0.9
1×0.1
2=0.027------(12分)
分析:设事件A:选报法语课;事件B:选报日语课.由题设知,事件A与B相互独立,且P(A)=0.75.P(B)=0.6
(1)法一:任选1名同学,该人一门课程均没选报的概率是
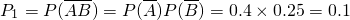
,由此能求出该人选报过第二外语的概率.
法二:任选1名同学,该人只选报一门课程的概率是

该人选报两门课程的概率是P
4=P(A•B)=0.75×0.6=0.45.由此能求出该人选报过第二外语的概率.
(2)【理科】因为每个人的选报是相互独立的,所以3人中选报过第二外语的人数ξ服从二项分布B(3,0.9),P(ξ=k)=C
3k×0.9
k×0.1
3-k,k=0,1,2,3,由此能求出ξ的分布列和ξ的期望Eξ及ξ的方差是Dξ.
【文科】3人中有1人选报过第二外语的概率为C
31×0.9
1×0.1
2=0.027.
点评:本题考查概率的求法,考查离散型分布列的求法和数学期望的计算,解题时要认真审题,仔细解答,注意二项分布知识的灵活运用.

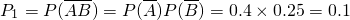

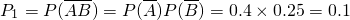 ,由此能求出该人选报过第二外语的概率.
,由此能求出该人选报过第二外语的概率.

