
分析 (1)设圆心坐标为(-1,b),则r=$\sqrt{4+(2-b)^{2}}$=$\sqrt{0+(2\sqrt{2}-b)^{2}}$,求出圆心与半径,即可求圆的方程;
(2)若过点P(-1,2)的弦AB长为2$\sqrt{7}$,则圆心到直线的距离d=$\sqrt{8-7}$=1,即可求直线AB的方程.
解答 解:(1)设圆心坐标为(-1,b),则r=$\sqrt{4+(2-b)^{2}}$=$\sqrt{0+(2\sqrt{2}-b)^{2}}$,
∴b=0,r=2$\sqrt{2}$,
∴圆的方程为(x+1)2+y2=8;
(2)过点P(-1,2)的弦AB长为2$\sqrt{7}$,则圆心到直线的距离d=$\sqrt{8-7}$=1,
设直线方程为y-2=k(x+1),即kx-y+k+2=0,
∴$\frac{2}{\sqrt{{k}^{2}+1}}$=1,∴k=±1,
∴直线AB的方程为x+y-1=0或x-y+3=0.
点评 本题考查圆的方程,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 关于点$({\frac{π}{3},0})$对称 | B. | 关于点$({\frac{2π}{3},0})$对称 | ||
| C. | 关于直线$x=\frac{π}{3}$对称 | D. | 关于直线$x=\frac{π}{6}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 20 | 40 | 20 | 10 | 10 |
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 10 | 20 | 20 | 40 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}+\frac{i}{2}$ | B. | $-\frac{1}{2}-\frac{i}{2}$ | C. | $\frac{1}{2}-\frac{i}{2}$ | D. | $\frac{1}{2}+\frac{i}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | $\frac{1}{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
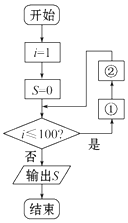
| A. | ①S=S+i ②i=i+1 | B. | ①S=S+i2 ②i=i+1 | C. | ①i=i+1 ②S=S+i | D. | ①i=i+1 ②S=S+i2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com