
(06年湖北卷文)(13分)
设![]() 分别为椭圆
分别为椭圆![]() 的左、右顶点,椭圆长半轴的长等于焦距,且
的左、右顶点,椭圆长半轴的长等于焦距,且![]() 为它的右准线。
为它的右准线。
(Ⅰ)、求椭圆的方程;
(Ⅱ)、设![]() 为右准线上不同于点(4,0)的任意一点,若直线
为右准线上不同于点(4,0)的任意一点,若直线![]() 分别与椭圆相交于异于
分别与椭圆相交于异于![]() 的点
的点![]() ,证明点
,证明点![]() 在以
在以![]() 为直径的圆内。
为直径的圆内。
(此题不要求在答题卡上画图)
解析:(I)依题意得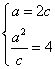 解得
解得![]() 从而b=
从而b=![]() ,
,
故椭圆方程为![]() 。
。
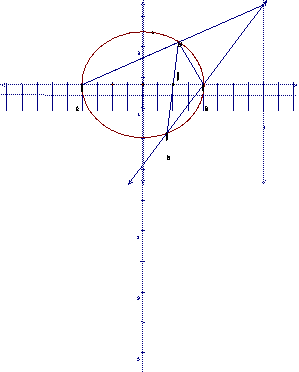
(II)解法1:由(I)得A(-2,0),B(2,0)。设![]() 。
。
![]() 点在椭圆上,
点在椭圆上,![]() 。
。
又![]() 点异于顶点
点异于顶点![]()
曲![]() 三点共线可得
三点共线可得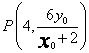 .
.
从面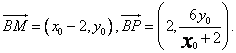
![]() .
.
将①式代入②式化简得![]()
![]() >0,
>0,![]() >0.于是
>0.于是![]() 为锐角,从而
为锐角,从而![]() 为钝角,故点
为钝角,故点![]() 在以
在以![]() 为直径的圆内.
为直径的圆内.
解法2:由(Ⅰ)得A(-2,0),B(2,0).设P(4,![]() )(
)(![]()
![]() 0),M(
0),M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),则直线AP的方程为
),则直线AP的方程为![]() ,直线BP的方程为
,直线BP的方程为![]() 。
。
![]() 点M、N分别在直线AP、BP上,
点M、N分别在直线AP、BP上,
![]()
![]() =
=![]() (
(![]() +2),
+2),![]() =
=![]() (
(![]() -2).从而
-2).从而![]()
![]() =
=![]() (
(![]() +2)(
+2)(![]() -2).③
-2).③
联立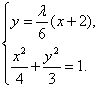 消去y得(27+
消去y得(27+![]() )
)![]() +4
+4![]() x+4(
x+4(![]() -27)=0.
-27)=0.
![]()
![]() ,-2是方程得两根,
,-2是方程得两根,![]() (-2).
(-2).![]() ,即
,即![]() =
=![]() . ④
. ④
又![]() .
.![]() =(
=(![]() -2,
-2, ![]() ).(
).(![]() -2,
-2,![]() )=(
)=(![]() -2)(
-2)(![]() -2)+
-2)+![]()
![]() . ⑤
. ⑤
于是由③、④式代入⑤式化简可得
![]() .
.![]() =
=![]() (
(![]() -2).
-2).
![]() N点在椭圆上,且异于顶点A、B,
N点在椭圆上,且异于顶点A、B,![]()
![]() <0.
<0.
又![]()
![]() ,
,![]()
![]() > 0, 从而
> 0, 从而![]() .
.![]() <0.
<0.
故![]()
![]() 为钝角,即点B在以MN为直径的圆内.
为钝角,即点B在以MN为直径的圆内.
解法3:由(Ⅰ)得A(-2,0),B(2,0).设M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),则-2<
),则-2<![]() <2 , -2<
<2 , -2<![]() <2.又MN的中点Q的坐标为(
<2.又MN的中点Q的坐标为(![]() ),
),
![]()
化简得![]() -
-![]()
![]() =(
=(![]() -2)(
-2)(![]() -2)+
-2)+![]()
![]() . ⑥
. ⑥
直线AP的方程为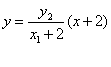 ,直线BP的方程为
,直线BP的方程为![]() .
.
![]() 点P在准线x=4上,
点P在准线x=4上,
![]()
![]() ,即
,即![]() . ⑦
. ⑦
又![]() M点在椭圆上,
M点在椭圆上,![]()
![]() +
+![]() =1,即
=1,即![]() ⑧
⑧
于是将⑦、⑧式化简可得![]() -
-![]()
![]() =
=![]()
![]() .
.
从而B在以MN为直径的圆内.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
(06年湖北卷文)(12分)
设向量a=(sinx,cosx),b=(cosx,cosx),x∈R,函数f(x)=a?(a+b).
(Ⅰ)求函数f(x)的最大值与最小正周期;
(Ⅱ)求使不等式f(x)≥![]() 成立的x的取值集。
成立的x的取值集。
查看答案和解析>>
科目:高中数学 来源: 题型:
(06年湖北卷文)(13分)
设数列![]() 的前n项和为
的前n项和为![]() ,点
,点![]() 均在函数y=3x-2的图像上。
均在函数y=3x-2的图像上。
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,
,![]() 是数列
是数列![]() 的前n项和,求使得
的前n项和,求使得![]() 对所有
对所有![]() 都成立的最小正整数m。
都成立的最小正整数m。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com