Question

设f(x)是(－∞，＋∞)上的奇函数，f(x＋2)＝－f(x)，当0≤x≤1时，f(x)＝x.

（1）求f(π)的值； 

（2）当－4≤x≤4时，求f(x)的图象与x轴所围成图形的面积；

（3）写出(－∞，＋∞)内函数f(x)的单调区间．

 

Answer 1

【答案】

（1）π－4.

（2）4

（3）递增区间为[4k－1,4k＋1](k∈Z)，单调递减区间[4k＋1,4k＋3](k∈Z)

【解析】

试题分析：解：(1)由f(x＋2)＝－f(x)得，

f(x＋4)＝f[(x＋2)＋2]＝－f(x＋2)＝f(x)，

所以f(x)是以4为周期的周期函数，

∴f(π)＝f(－1×4＋π)＝f(π－4)＝－f(4－π)＝－(4－π)＝π－4.

(2)由f(x)是奇函数与f(x＋2)＝－f(x)，得：f[(x－1)＋2]＝－f(x－1)＝f[－(x－1)]，即f(1＋x)＝f(1－x)．

故知函数y＝f(x)的图象关于直线x＝1对称．

又0≤x≤1时，f(x)＝x，且f(x)的图象关于原点成中心对称，则f(x)的图象如图所示．

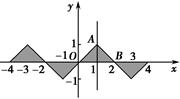
当－4≤x≤4时，f(x)的图象与x轴围成的图形面积为S，则

S＝4S_△OAB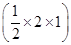＝4×＝4.

(3)根据（1）（2）可知函数的图形，根据奇偶性以及解析式和对称中心可知，

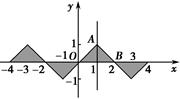
在一个周期[-1,3]内的图象可知增区间为[-1,1]，减区间为[1,3],那么推广到整个实数域可知，都加上周期的整数倍即可，故可知函数f(x)的单调递增区间为[4k－1,4k＋1](k∈Z)，单调递减区间[4k＋1,4k＋3](k∈Z)

考点：函数图象与性质

点评：主要是考查了函数的图象与性质的综合运用，属于中档题。