
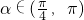 ,
, ,则tanα=________.
,则tanα=________.
 ,π),得到sinα大于cosα,即sinα-cosα大于0,进而求出sinα-cosα的值,记作②,联立①②即可求出sinα和cosα的值,然后再利用同角三角函数间的基本关系,即可求出tanα的值.
,π),得到sinα大于cosα,即sinα-cosα大于0,进而求出sinα-cosα的值,记作②,联立①②即可求出sinα和cosα的值,然后再利用同角三角函数间的基本关系,即可求出tanα的值. ,π),得到sinα>cosα,即sinα-cosα>0,
,π),得到sinα>cosα,即sinα-cosα>0, ①两边平方得:1+2sinαcosα=
①两边平方得:1+2sinαcosα= ,即2sinαcosα=
,即2sinαcosα= ,
, ,即(sinα-cosα)2=
,即(sinα-cosα)2= ,即sinα-cosα=
,即sinα-cosα= ②,
②, ,cosα=
,cosα= ,
, =
= .
.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com