A
分析:由对数函数的定义可知真数大于0,根据分母不为0,由对数的运算法则得到真数不为1,真数大于0列出不等式,根据基本不等式变形,得到关于m的不等式,求出不等式的解集得到m的取值范围;根据真数不为1,设t=5
x,把不等式变形,若根的判别式小于0,方程无解,满足题意,列出关于m的不等式,求出不等式的解集得到m的范围,若方程有负数解也满足题意,故根据韦达定理得到两根之积为4大于0,从而得到两根之和应小于0,列出关于m的不等式,得到m的范围,综上,求出所有范围的并集即可得到实数m的范围.
解答:∵5
x>0,∴5
x+
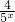
≥4,当且仅当5
x=
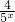
,即x=log
52时取等号,
根据负数和0没有对数得:5
x+
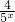
+m≥4+m>0,解得m>-4,
又根据分母不为0得到:5
x+
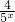
+m≠1,令5
x=t>0,化为t+

+m≠1,
∵t>0,∴当t
2+(m-1)t+4=0没有解或解为负数时,t
2+(m-1)t+4≠0,
若△=(m-1)
2-16<0,解得:-3<m<5,方程无解,满足题意;
若t
2+(m-1)t+4=0没有正数解,根据两根之积为4>0,得到两根为同号,
故要保证两根为负数,需两根之和1-m<0,解得m>1,
综上,实数m的范围是m>-3,
则实数m的取值范围是(-3,+∞).
故选A
点评:此题考查了对数函数的定义域,求对数函数定义域时注意真数大于0且分母不为0.解答此题时运用了基本不等式,韦达定理,以及换元的思想,要求学生掌握知识要全面,考虑问题要周全.

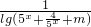 的定义域为R,则实数m的取值范围是
的定义域为R,则实数m的取值范围是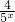 ≥4,当且仅当5x=
≥4,当且仅当5x=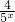 ,即x=log52时取等号,
,即x=log52时取等号,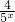 +m≥4+m>0,解得m>-4,
+m≥4+m>0,解得m>-4,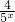 +m≠1,令5x=t>0,化为t+
+m≠1,令5x=t>0,化为t+ +m≠1,
+m≠1,

 阅读快车系列答案
阅读快车系列答案