Question

若F_l、F₂为双曲线C：=1的左、右焦点，O为坐标原点，点P及N(2,)均在双曲线c上，M在C的右准线上，且满足

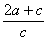
(1)求双曲线C的离心率及其方程；

(2)设双曲线C的虚轴端点为B₁、B2(B₁在y轴的正半轴上)，点A、B在双曲线上，且当=0时，求直线AB的方程．

Answer 1

解:(1)∵

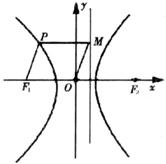
∴四边形OF₁PM为菱形．

设F₁(-c，0)，则|PF₁|=|PM|=c

由双曲线第一定义，得|PF₂|=2a+c

由双曲线第二定义，得=e,即=e

整理，得e²-e-2=0  解得e=2(e=-1舍去)

此时C的方程为=1，将N(2，)代入得，a²=3

∴双曲线方程为=1

(2)依题意B₁(0，3)，B₂(0，-3)

∵

∴ A、B、B₂三点共线，设其方程为y=kx-3．

由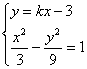  得(3-k²)x²+6kx-18=0．(*)，

设A(x₁，y₁)，B(x₂，y₂)，

∵k≠±  ∴x₁+x₂= ，x₁x₂= 

y₁+y₂=k(x₁+x₂)-6=，

y_ly₂=k²x₁x₂-3k(x₁+x₂)+9=9

∵=0   ∴(x_l，y₁-3)·(x₂，y₂-3)=0

∴x₁x₂+y₁y₂-3(y₁+y₂)+9=0

∴+9-3·+9=0，解得k=±

此时方程(*)中，△＞0．故所求直线方程为y=±x-3