
 ,设函数
,设函数 .
. ,且
,且 恰是函数f(x)在
恰是函数f(x)在 上的最大值,求A,b和三角形ABC的面积.
上的最大值,求A,b和三角形ABC的面积. ;(2)
;(2) ,
, 或
或 ,
,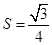 或
或 .
. 的解析式,利用降幂公式、倍角公式、两角和的正弦公式化简表达式,使之化简成
的解析式,利用降幂公式、倍角公式、两角和的正弦公式化简表达式,使之化简成 的形式,利用
的形式,利用 求函数的周期;第二问,先将
求函数的周期;第二问,先将 代入得到
代入得到 的范围,数形结合得到
的范围,数形结合得到 的最大值,并求出此时的角A,在三角形中利用余弦定理得到边b的值,最后利用
的最大值,并求出此时的角A,在三角形中利用余弦定理得到边b的值,最后利用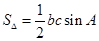 求三角形面积.
求三角形面积.


 4分
4分 ,所以最小正周期
,所以最小正周期 . 6分
. 6分 ,当
,当 时,
时, .
. 时,
时, 取得最大值
取得最大值 ,又
,又 为锐角
为锐角 . 8分
. 8分 得
得 ,所以
,所以 或
或
 时,△
时,△ 的面积
的面积 ; 11分
; 11分 时,
时, . 12分
. 12分

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com