Question

（）以知F是双曲线的左焦点，是双曲线右支上的动点，则的最小值为                                 。

Answer 1

9

（17）（本小题满分12分）

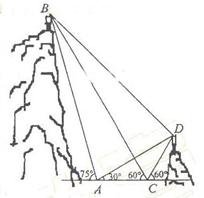如图，A,B,C,D都在同一个与水平面垂直的平面内，B，D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为，，于水面C处测得B点和D点的仰角均为，AC=0.1km。试探究图中B，D间距离与另外哪两点间距离相等，然后求B，D的距离（计算结果精确到0.01km，1.414，2.449）w.w.w.k.s.5.u.c.o.m       

(17)解:

在△ABC中，∠DAC=30°, ∠ADC=60°－∠DAC=30,

所以CD=AC=0.1 又∠BCD=180°－60°－60°=60°，

故CB是△CAD底边AD的中垂线，所以BD=BA，          ……5分

在△ABC中，

即AB=

因此，BD=

故B，D的距离约为0.33km。                         ……12分

（18）（本小题满分12分）

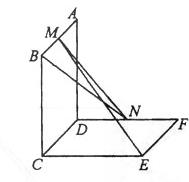
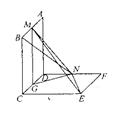
如图，已知两个正方行ABCD 和DCEF不在同一平面内，M，N分别为AB，DF的中点  。

（I）若平面ABCD ⊥平面DCEF，求直线MN与平面DCEF所成角的正值弦；

（II）用反证法证明：直线ME 与 BN 是两条异面直线。w.w.w.k.s.5.u.c.o.m       

（18）（I）解法一：

取CD的中点G，连接MG，NG。

设正方形ABCD，DCEF的边长为2，                

则MG⊥CD，MG=2，NG=.

因为平面ABCD⊥平面DCED，

所以MG⊥平面DCEF，

可得∠MNG是MN与平面DCEF所成的角。因为MN=，所以sin∠MNG=为MN与平面DCEF所成角的正弦值                                          ……6分

解法二：

  设正方形ABCD，DCEF的边长为2，以D为坐标原点，分别以射线DC，DF，DA为x,y,z轴正半轴建立空间直角坐标系如图.

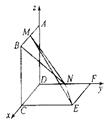则M（1,0,2）,N(0,1,0),可得=(－1,1,2).                      

又=（0，0，2）为平面DCEF的法向量，

可得cos(,)=·                

所以MN与平面DCEF所成角的正弦值为

cos·                                         ……6分

(Ⅱ)假设直线ME与BN共面，                                       ……8分

则AB平面MBEN，且平面MBEN与平面DCEF交于EN

由已知，两正方形不共面，故AB平面DCEF。

又AB//CD，所以AB//平面DCEF。面EN为平面MBEN与平面DCEF的交线，

所以AB//EN。

又AB//CD//EF，

所以EN//EF，这与EN∩EF=E矛盾，故假设不成立。

所以ME与BN不共面，它们是异面直线.                                  ……12分

（19）（本小题满分12分）

某人向一目射击4次，每次击中目标的概率为。该目标分为3个不同的部分，第一、二、三部分面积之比为1：3：6。击中目标时，击中任何一部分的概率与其面积成正比。

（Ⅰ）设X表示目标被击中的次数，求X的分布列；

（Ⅱ）若目标被击中2次，A表示事件“第一部分至少被击中1次或第二部分被击中2次”，求P（A）w.w.w.k.s.5.u.c.o.m       

（19）解：

（Ⅰ）依题意X的分列为

   

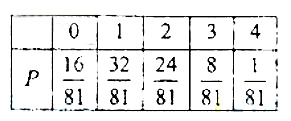
            ………………6分

（Ⅱ）设A₁表示事件“第一次击中目标时，击中第i部分”，i=1，2.

        B₁表示事件“第二次击中目标时，击中第i部分”，i=1，2.

依题意知P（A₁）=P(B₁)=0.1，P（A₂）=P(B₂)=0.3，

,

所求的概率为

      

                   ………12分

 

（20）（本小题满分12分）

已知，椭圆C过点A，两个焦点为（－1，0），（1，0）。

（1）       求椭圆C的方程；w.w.w.k.s.5.u.c.o.m       

（2）       E,F是椭圆C上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明直线EF的斜率为定值，并求出这个定值。

（20）解：

（Ⅰ）由题意，c=1,可设椭圆方程为，解得，（舍去）

所以椭圆方程为。                                 ……………4分

（Ⅱ）设直线AE方程为：，代入得

 设,,因为点在椭圆上，所以

              

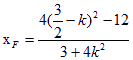
                                         ………8分

又直线AF的斜率与AE的斜率互为相反数，在上式中以—K代K，可得

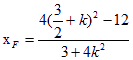
所以直线EF的斜率

即直线EF的斜率为定值，其值为。                  ……12分

（21）（本小题满分12分）

已知函数f(x)=x－ax+(a－1)，。

（1）讨论函数的单调性；w.w.w.k.s.5.u.c.o.m       

（2）证明：若，则对任意x，x，xx，有。

(21)解：(1)的定义域为。

2分

（i）若即,则

故在单调增加。

(ii)若,而,故,则当时，;

当及时，

故在单调减少，在单调增加。

(iii)若,即,同理可得在单调减少，在单调增加.

(II)考虑函数

则

由于1<a<5,故，即g(x)在(4, +∞)单调增加，从而当时有，即，故，当时，有·········12分

请考生在第（22）、（23）、（24）三题中任选一题做答，如果多做，则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目的题号涂黑。

（22）（本小题满分10分）选修4－1：几何证明讲w.w.w.k.s.5.u.c.o.m       

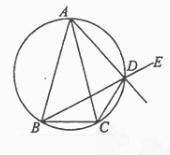已知 ABC   中，AB=AC,  D是 ABC外接圆劣弧上的点（不与点A,C重合），延长BD至E。

（1）       求证：AD的延长线平分CDE；

（2）       若BAC=30，ABC中BC边上的高为2+，求ABC外接圆的面积。w.w.w.k.s.5.u.c.o.m       

（22）解：

（Ⅰ）如图，设F为AD延长线上一点

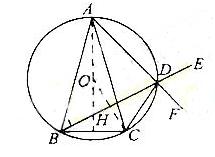∵A，B，C，D四点共圆，

∴∠CDF=∠ABC

又AB=AC  ∴∠ABC=∠ACB,

且∠ADB=∠ACB, ∴∠ADB=∠CDF,

对顶角∠EDF=∠ADB, 故∠EDF=∠CDF,

即AD的延长线平分∠CDE.

（Ⅱ）设O为外接圆圆心，连接AO交BC于H,则AH⊥BC.

    连接OC,A由题意∠OAC=∠OCA=15⁰, ∠ACB=75⁰,

∴∠OCH=60⁰.

设圆半径为r,则r+r=2+,a得r=2,外接圆的面积为4。

（23）（本小题满分10分）选修4－4 ：坐标系与参数方程在直角坐标系xOy中，以O为极点，x正半轴为极轴建立极坐标系，曲线C的极坐标方程为cos（）=1，M,N分别为C与x轴，y轴的交点。

（1）写出C的直角坐标方程，并求M,N的极坐标；w.w.w.k.s.5.u.c.o.m       

（2）设MN的中点为P，求直线OP的极坐标方程。

（23）解：

（Ⅰ）由

     

从而C的直角坐标方程为

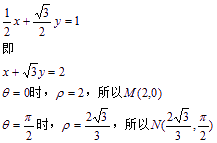
（Ⅱ）M点的直角坐标为（2，0）

N点的直角坐标为

所以P点的直角坐标为

所以直线OP的极坐标方程为

（24）（本小题满分10分）选修4－5：不等式选讲

设函数。

（1）       若解不等式；

（2）如果,,求 的取值范围。w.w.w.k.s.5.u.c.o.m       

（24）解：

（Ⅰ）当a=－1时，f(x)=︱x－1︳+︱x+1︳.

由f(x)≥3得

︱x－1︳+︱x+1|≥3

（ⅰ）x≤－1时，不等式化为

1－x－1－x≥3 即－2x≥3

解析:

注意到P点在双曲线的两只之间,且双曲线右焦点为F’(4,0),

        于是由双曲线性质|PF|－|PF’|＝2a＝4

        而|PA|＋|PF’|≥|AF’|＝5

        两式相加得|PF|＋|PA|≥9,当且仅当A、P、F’三点共线时等号成立.