已知直线l1:(m+2)x+(m+3)y-5=0和直线l2:6x+(2m-1)=5,求满足下列条件的实数m的取值范围或取值:
(1)l1∥l2;
(2)l1⊥l2.
【答案】
分析:(1)l
1:(m+2)x+(m+3)y-5=0和直线l
2:6x+(2m-1)=5,由l
1∥l
2,知
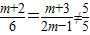
,由此能求出m.
(2)l
1:(m+2)x+(m+3)y-5=0和直线l
2:6x+(2m-1)=5,由l
1⊥l
2,知6(m+2)+(2m-1)(m+3)=0,由此能求出m.
解答:解:(1)l
1:(m+2)x+(m+3)y-5=0和直线l
2:6x+(2m-1)=5,
∵l
1∥l
2,∴
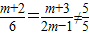
,
解得m=-

,m=4(舍),
故m=-

.
(2)l
1:(m+2)x+(m+3)y-5=0和直线l
2:6x+(2m-1)=5,
∵l
1⊥l
2,∴6(m+2)+(2m-1)(m+3)=0,
解得m=-1,或m=-

.
点评:本题考查直线的平行和垂直关系的条件和应用,是基础题.解题时要认真审题,仔细解答.

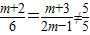 ,由此能求出m.
,由此能求出m.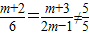 ,
, ,m=4(舍),
,m=4(舍), .
. .
.

 名校课堂系列答案
名校课堂系列答案