练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

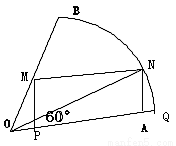
    在圆心角为60°的扇形铁板OAB中，工人师傅要裁出一个面积最大的内接矩形，求此内接矩形的最大面积。

     

    【答案】

    当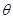=30°时，矩形的面积最大，其最大值是.

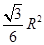    【解析】

    试题分析：要找出内接矩形的长宽与面积S的关系，可采用引入第三个变量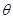的办法，用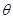表示矩形的长宽x，y，这样矩形的面积可以表示成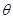的三角函数，通过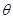的变化情况，得出S的最大值。

    解：如图，设PQ=x，MP=y，则矩形面积S=xy

    连接ON，令∠AON=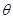，则y=Rsin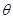

    在三角形OMN中：由正弦定理得：

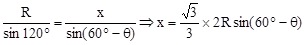
    S=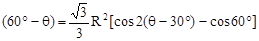

    故当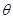=30°时，矩形的面积最大，其最大值是.

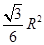    考点：本题主要考查正弦定理的应用，两角和与差的三角函数公式。

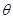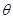    点评：分析几何图形的特征，可以发现，要找出内接矩形的长宽与面积S的关系，可采用引入第三个变量的办法，用表示矩形的长宽x，y，这样矩形的面积可以表示成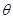的三角函数，通过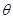的变化情况，得出S的最大值。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

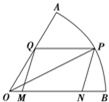    精英家教网如图，现在要在一块半径为1m．圆心角为60°的扇形纸板AOB上剪出一个平行四边形MNPQ，使点P在AB弧上，点Q在OA上，点M，N在OB上，设∠BOP=θ．平行四边形MNPQ的面积为S．
    （1）求S关于θ的函数关系式；
    （2）求S的最大值及相应θ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图，在半径为
    		3
    、圆心角为60°的扇形的弧上任取一点P，作扇形的内接矩形PNMQ，使点Q在OA上，点（N，M）在OB上，设矩形PNMQ的面积为y，
    （1）按下列要求写出函数的关系式：
     ①设PN=x，将y表示成x的函数关系式；
     ②设∠POB=θ，将y表示成θ的函数关系式；
    （2）请你选用（1）中的一个函数关系式，求出y的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

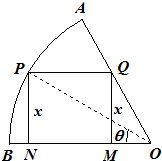
    如图，在半径为R、圆心角为60°的扇形AB弧上任取一点P，作扇形的内接矩形PNMQ，使点Q在OA上，点M，N在OB上，设∠BOP=θ，矩形PNMQ的面积记为S．
    （1）求S与θ之间的函数关系式；
    （2）求矩形PNMQ面积的最大值及相应的θ值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2009•武昌区模拟）如图，在半径为
    		6
    cm，圆心角为60°的扇形OAB中，点C为弧AB的中点，按如图截出一个内接矩形，则矩形的面积为
    		3
    		3
    cm2．

    查看答案和解析>>

    同步练习册答案