
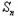 =
= n2﹣
n2﹣ n.数列{
n.数列{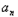 }满足(
}满足(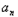 )3=4﹣(bn+2),n∈N*,数列{cn}满足cn=
)3=4﹣(bn+2),n∈N*,数列{cn}满足cn=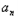 bn.
bn. m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.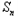 ﹣
﹣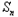 ﹣1=(
﹣1=( n2﹣
n2﹣ n)﹣[
n)﹣[ (n﹣1)2﹣
(n﹣1)2﹣ (n﹣1)]=3n﹣2
(n﹣1)]=3n﹣2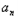 }满足(
}满足(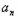 )3=4﹣(bn+2)
)3=4﹣(bn+2)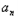 )3=4﹣3n,
)3=4﹣3n,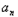 =4﹣n,
=4﹣n,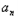 bn=(3n﹣2)×4﹣n,
bn=(3n﹣2)×4﹣n, Tn=1×4﹣2+4×4﹣3+…+(3n﹣2)×4﹣n﹣1,②
Tn=1×4﹣2+4×4﹣3+…+(3n﹣2)×4﹣n﹣1,② Tn=4﹣1+3[4﹣2+4﹣3+…+4﹣n]﹣(3n﹣2)×4﹣n﹣1=
Tn=4﹣1+3[4﹣2+4﹣3+…+4﹣n]﹣(3n﹣2)×4﹣n﹣1= ﹣(3n﹣2)×4﹣n﹣1,
﹣(3n﹣2)×4﹣n﹣1, ﹣
﹣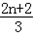 ×4﹣n;
×4﹣n; 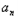 bn=(3n﹣2)×4﹣n,
bn=(3n﹣2)×4﹣n,
 m2+m﹣1对一切正整数n恒成立,则
m2+m﹣1对一切正整数n恒成立,则 m2+m﹣1≥
m2+m﹣1≥ 即可,
即可,

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn-1 |
| an+1 |
| an+1 |
| bn |
| bn+1 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 10 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | anan+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com