
【题目】如图,圆柱体木材的横截面半径为![]() ,从该木材中截取一段圆柱体,再加工制作成直四棱柱
,从该木材中截取一段圆柱体,再加工制作成直四棱柱![]() ,该四棱柱的上、下底面均为等腰梯形,分别内接于圆柱的上、下底面,下底面圆的圆心
,该四棱柱的上、下底面均为等腰梯形,分别内接于圆柱的上、下底面,下底面圆的圆心![]() 在梯形
在梯形![]() 内部,
内部,![]() ,
,![]() ,
,![]() ,设
,设![]() .
.
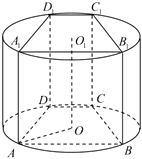
(1)求梯形![]() 的面积;
的面积;
(2)当![]() 取何值时,直四棱柱
取何值时,直四棱柱![]() 的体积最大?并求出最大值(注:木材的长度足够长)
的体积最大?并求出最大值(注:木材的长度足够长)
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() x3+ax2+bx,且f′(﹣1)=0.
x3+ax2+bx,且f′(﹣1)=0.
(1)试用含a的代数式表示b;
(2)求f(x)的单调区间;
(3)令a=﹣1,设函数f(x)在x1、x2(x1<x2)处取得极值,记点M(x1,f(x1)),N(x2,f(x2)).证明:线段MN与曲线f(x)存在异于M,N的公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校要在一条水泥路边安装路灯,其中灯杆的设计如图所示,AB为地面,CD,CE为路灯灯杆,CD⊥AB,∠DCE=![]() ,在E处安装路灯,且路灯的照明张角∠MEN=
,在E处安装路灯,且路灯的照明张角∠MEN=![]() .已知CD=4m,CE=2m.
.已知CD=4m,CE=2m.
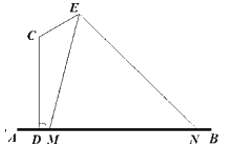
(1)当M,D重合时,求路灯在路面的照明宽度MN;
(2)求此路灯在路面上的照明宽度MN的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() ,
,![]() ),
),![]() 和
和![]() 是函数
是函数![]() 的图象与
的图象与![]() 轴的2个相邻交点的横坐标,且当
轴的2个相邻交点的横坐标,且当![]() 时,
时,![]() 取得最大值2.
取得最大值2.
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)将函数![]() 的图象上的每一点的横坐标变为原来的
的图象上的每一点的横坐标变为原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象,再将函数
的图象,再将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求函数
的图象,求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(2)是否存在实数![]() ,使得对任意
,使得对任意![]() ,存在
,存在![]() ,不等式
,不等式![]() 成立?若存在,求出
成立?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com