练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图1-3-16，已知△ABC中，DE∥FG∥BC，AD∶DF∶FB=2∶3∶4，

    求S△ADE∶S四边形DEGF∶S四边形BCGF.

    图1-3-16

    思路分析:要求题目中的三部分的面积比，必须先求出△ADE\,△AFG和△ABC的面积，才能求出两个四边形的面积.由已知DE∥FG∥BC的条件，可以得到相似三角形，再由相似三角形的面积比等于相似比的平方的性质，可求出相似三角形的面积比.题目中未给出具体数值，故应引入参数.

    解：∵AD∶DF∶FB=2∶3∶4，

    设AD=2k,DF=3k,FB=4k(k＞0)，则AF=5k,AB=9k,

    ∵DE∥FG,∴△ADE∽△AFG.

    ∴

    同理,可得.

    设S△ADE=4a,则S△AFG=25a,S△ABC=81a(a＞0).

    ∴S四边形DEGF=25a-4a=21a，

    S四边形BCGF=81a-25a=56a.

    ∴S△ADE∶S四边形DEGF∶S四边形BCGF=4∶21∶56.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

    如图1-3-16,已知Rt△ABC中,D是斜边AB的中点,DE⊥AB于D,交AC于F,交BC延长线于E,BG⊥BA,交DC延长线于H,交AC延长线于G.?

    图1-3-16

    求证:(1)GH·CE =DF·BC;?

    (2)DC2=DF·DE;?

    (3)CH·CD =GH·DE;?

    (4)GB∶BA =CH∶BH;?

    (5)CH·EF =BA·DF.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图1-2-3,已知l1∥l2∥l3,AM=3,BM=5,CM=4.5,EF=16.

    图1-2-3

    求DM、EK、FK的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某企业甲将经营状态良好的某种消费品专卖店以58万元的优惠价转让给企业乙，约定乙用经营该店的利润偿还转让费（不计息）。已知经营该店的固定成本为6.8万元/月，该消费品的进价为16元/件，月销量q（万件）与售价p(元/件)的关系如图.

    (1）写出销量q与售价p的函数关系式；

    （2）当售价p定为多少时，月利润最多？

    （3）企业乙最早可望在经营该专卖店几个月后还清转让费？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

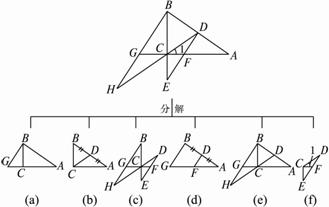
    如图1-3-16,已知Rt△ABC中,D是斜边AB的中点,DE⊥AB于D,交AC于F,交BC延长线于E,BG⊥BA,交DC延长线于H,交AC延长线于G.

    图1-3-16

    求证:(1)GH·CE =DF·BC;

    (2)DC2=DF·DE;

    (3)CH·CD =GH·DE;

    (4)GB∶BA =CH∶BH;

    (5)CH·EF =BA·DF.

    查看答案和解析>>

    同步练习册答案