
 已知函数
已知函数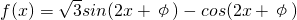 (0<φ<π)
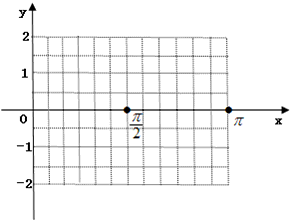
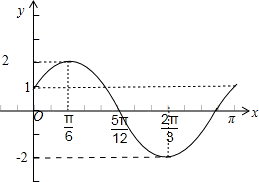
(0<φ<π) ,用“五点法”在给定的坐标系中,画出函数f(x)在[0,π]上的图象.
,用“五点法”在给定的坐标系中,画出函数f(x)在[0,π]上的图象. 个单位后,再将得到的图象上各点的横坐标变为原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)在[0,π]的单调递减区间.
个单位后,再将得到的图象上各点的横坐标变为原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)在[0,π]的单调递减区间. 时,
时,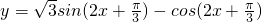 =
=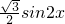 +
+ cos2x-
cos2x- cos2x+
cos2x+ sin2x=
sin2x= sin2x+cos2x=
sin2x+cos2x= ,
, 2x+ |  |  | π |  | 2π |  |
| x | 0 |  |  |  |  | π |
| y | 1 | 2 | 0 | -2 | 0 | 1 |
 (6分)
(6分)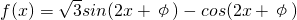 =
=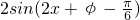 ,…(8分)
,…(8分)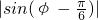 =1,则
=1,则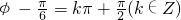 ,即
,即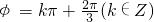 .
.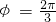 . …(11分)
. …(11分) )=cos2x,
)=cos2x, 个单位,可得函数f(x-
个单位,可得函数f(x- )的图象,再把所得的图象上各个点的横坐标变为原来的4倍,
)的图象,再把所得的图象上各个点的横坐标变为原来的4倍, -
- )的图象,故g(x)=f(
)的图象,故g(x)=f( -
- )=2cos(
)=2cos( -
- ).
). -
- ≤2kπ+π,k∈z,解得 4kπ+
≤2kπ+π,k∈z,解得 4kπ+ ≤x≤2kπ+
≤x≤2kπ+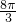 ,
, ,2kπ+
,2kπ+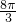 ],k∈z.
],k∈z. 时,化简函数f(x)的解析式,用五点法作出函数y=f(x)在区间[0,π]上的图象.
时,化简函数f(x)的解析式,用五点法作出函数y=f(x)在区间[0,π]上的图象.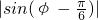 =1,再根据φ的范围,求得φ的值.
=1,再根据φ的范围,求得φ的值. -
- )=2cos(
)=2cos( -
- ).令2kπ≤
).令2kπ≤ -
- ≤2kπ+π,k∈z,求得x的范围,即可求得g(x)的单调减区间.
≤2kπ+π,k∈z,求得x的范围,即可求得g(x)的单调减区间.

科目:高中数学 来源:2009-2010学年黑龙江省鹤岗一中高一(上)期末数学试卷(文科)(解析版) 题型:解答题
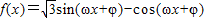 (0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
(0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为 .
.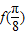 的值;
的值;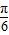 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.查看答案和解析>>
科目:高中数学 来源:广东省09-10学年高二下学期期末考试数学试题(文科卷) 题型:解答题
(满分14分)已知函数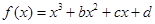 在(-
在(-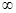 ,0)上是增函数,在[0,2]上是减函数,且方程
,0)上是增函数,在[0,2]上是减函数,且方程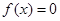 有三个根分别为
有三个根分别为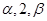 .
.
(1)求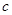 的值;
的值;
(2)求证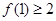 ;
;
(3)求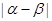 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年贵州省7校高三联考理数试题 题型:填空题
(本小题满分12分)
已知函数 在[0,+
在[0,+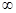 )上最小值是
)上最小值是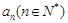
(1)求数列 的通项公式;
的通项公式;
(2)令 ,求证:
,求证: ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com