
 如图,在平行六面体ABCD-A1B1C1D1中,M为AC与D的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{A{{\;}_{1}D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{{C}_{1}M}$.
如图,在平行六面体ABCD-A1B1C1D1中,M为AC与D的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{A{{\;}_{1}D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{{C}_{1}M}$. 分析 根据空间向量的线性运算的几何意义,利用平行六面体的性质,用向量$\overrightarrow{{A}_{1}{B}_{1}}$、$\overrightarrow{A{{\;}_{1}D}_{1}}$和$\overrightarrow{{A}_{1}A}$表示出向量$\overrightarrow{{C}_{1}M}$即可.
解答 解:平行六面体ABCD-A1B1C1D1中,$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{A{{\;}_{1}D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,
∴$\overrightarrow{CM}$=$\frac{1}{2}$$\overrightarrow{CA}$=$\frac{1}{2}$($\overrightarrow{CB}$+$\overrightarrow{CD}$)=$\frac{1}{2}$$\overrightarrow{CB}$+$\frac{1}{2}$$\overrightarrow{CD}$
∴向量$\overrightarrow{{C}_{1}M}$=$\overrightarrow{CM}$-$\overrightarrow{{CC}_{1}}$
=$\frac{1}{2}$$\overrightarrow{CB}$+$\frac{1}{2}$$\overrightarrow{CD}$-$\overrightarrow{{CC}_{1}}$
=$\frac{1}{2}$$\overrightarrow{{{D}_{1}A}_{1}}$+$\frac{1}{2}$$\overrightarrow{{{B}_{1}A}_{1}}$-$\overrightarrow{{AA}_{1}}$
=-$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{c}$
=-$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$.
点评 本题考查了空间向量的线性运算的几何意义与应用问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | P(x,y,z)中x,y,z的位置可以互换的 | |
| B. | 空间直角坐标系中的点与一个三元有序数组是一种一一对应关系 | |
| C. | 空间直角坐标系中的三条坐标轴把空间分成八个部分 | |
| D. | 某点在不同空间直角坐标系中的坐标位置可以相同 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{6}$,$\frac{1}{3}$) | B. | (0,$\frac{1}{3}$) | C. | (0,$\frac{1}{6}$] | D. | ($\frac{1}{3}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
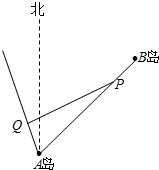 已知海岛B在海岛A的北偏东45°的方向上,两岛相距10海里.小船P从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船Q从海岛A出发,沿北偏西15°方向以4海里/小时的速度移动.
已知海岛B在海岛A的北偏东45°的方向上,两岛相距10海里.小船P从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船Q从海岛A出发,沿北偏西15°方向以4海里/小时的速度移动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com