练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    （1）若四边形ABCD的对角线AC将四边形分成面积相等的两个三角形，证明直线AC必平分对角线BD．
    （2）写出（1）的逆命题，这个逆命题是否正确？为什么？

    精英家教网
    （1）证：S△ABC=S△ADC′
    且△ABC与△ADC有同底AC，
    ∴两高线相等：BE=DF
    设AC与BD交于点O，
    则Rt△BOE≌Rt△DOF，∴OB=OD，即AC平分BD．

    （2）逆命题：若四边形ABCD的对角线AC平分对角线BD，
    则AC必将四边形分成两个面积相等的三角形这个逆命题是正确的．
    证明如下：在图中，由于OB=OD，∠BOE=∠DOF
    ，∠BEO=∠DFO=Rt∠，∴△BOE≌△DOF．
    ∴BE=DF，即两高线相等．∴S△ABC=
    1
    2
    AC?BE=
    1
    2
    AC?DF=S△ADC'．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    2、下列命题中：
    （1）命题“在△ABC中，若AB＞AC，则∠C＞∠B”的逆命题；
    （2）命题“若ab=0，则a≠0且b=0”的否命题；
    （3）若题“若a≠0且b≠0，则ab≠0”的逆否命题；
    （4）命题“平行四边形的两条对角线互相平分”的逆命题；
    其中是真命题的个数是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

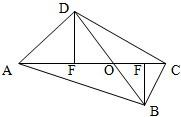
    设△ABC的外心为O，以线段OA、OB为邻边作平行四边形，第四个顶点为D，再以OC、OD为邻边作平行四边形，它的第四个顶点为H．
    （1）若
    OA
    =
    a
    ，
    OB
    =
    b
    ，
    OC
    =
    c
    ，用
    a
    、
    b
    、
    c
    表示
    OH
    ；
    （2）求证：AH⊥BC；
    （3）设△ABC中，∠A=60°，∠B=45°，外接圆半径为R，用R表示
    |OH|
    ．（外心是三角形外接圆的圆心）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在三棱柱ABC-A1B1C1中，∠ACB=120°，AC=CB=1，D1是线段A1B1上一动点（可以与A1或B1重合）．过D1和CC1的平面与AB交于D．
    （1）若四边形CDD1C1总是矩形，求证：三棱柱ABC-A1B1C1为直三棱柱；
    （2）在（1）的条件下，求二面角B-AD1-C的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年江西省高三实验班第五次月考数学 题型：解答题

    （本题满分12分）

    在三棱柱ABC-A1B1C1中，∠ACB=，AC=CB=1，D1是线段A1B1上一动点（可以与A1或B1重合）。过D1和CC1的平面与AB交于D。

    (1）若四边形CDD1C1总是矩形，求证：三棱柱ABC-A1B1C1为直三棱柱；

    (2)在（1）的条件下，求二面角B-AD1-C的取值范围。

       

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年江西省赣南师院附中高三（上）10月月考数学试卷（实验班）（解析版） 题型：解答题

    在三棱柱ABC-A1B1C1中，∠ACB=120°，AC=CB=1，D1是线段A1B1上一动点（可以与A1或B1重合）．过D1和CC1的平面与AB交于D．
    （1）若四边形CDD1C1总是矩形，求证：三棱柱ABC-A1B1C1为直三棱柱；
    （2）在（1）的条件下，求二面角B-AD1-C的取值范围．

    查看答案和解析>>

    同步练习册答案