
| 1 |
| x |
| 1 |
| lgx |
| x2+3 | ||
|
| x |
| 1 | ||
|
| 1 |
| sin2x |
| π |
| 2 |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| lgx |
| x2+3 | ||
|
| x2+2+1 | ||
|
| x2+2 |
| 1 | ||
|
| x2+2 |
| 1 | ||
|
| x |
| 1 | ||
|
|
| 1 |
| sin2x |
| π |
| 2 |
| 1 |
| sin2x |
| π |
| 2 |
| 1 |
| x |
| 1 |
| x2 |
x2•
|


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
. |
| DA |
. |
| DC |
. |
| DB |
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修四2.2平面向量的线性运算练习卷(一)(解析版) 题型:选择题
已知平行四边形ABCD,设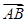 +
+ +
+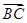 +
+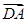 =a,而b是一非零向量,则下列结论正确的有( )
=a,而b是一非零向量,则下列结论正确的有( )
①a∥b ②a+b=a
③a+b=b ④|a+b|<|a|+|b|
A.①③ B.②③
C.②④ D.①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com