
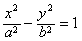 (a>0,b>0,xy≠0)上的动点,F1,F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且
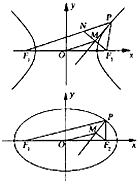
(a>0,b>0,xy≠0)上的动点,F1,F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且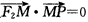 .某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2N的中点,得|OM|=
.某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2N的中点,得|OM|=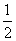 |NF1|=…=a。类似地:P是椭圆
|NF1|=…=a。类似地:P是椭圆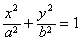 (a>b>0,xy≠0)上的动点,F1,F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且
(a>b>0,xy≠0)上的动点,F1,F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且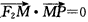 ,则|OM|的取值范围是( )。
,则|OM|的取值范围是( )。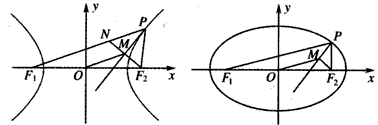
 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
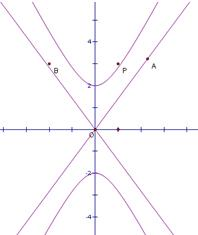 已知双曲线C的方程为
已知双曲线C的方程为| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
2
| ||
| 5 |
| AP |
| PB |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 我们定义双曲线C:
我们定义双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
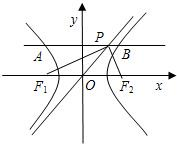
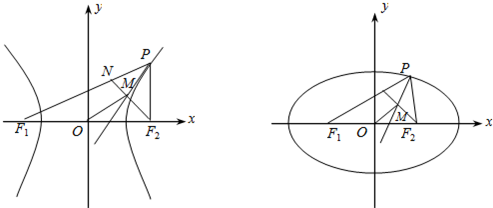
 如图,P是双曲线
如图,P是双曲线| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| F2M |
| MP |
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| F2M |
| MP |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com