


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:2015届四川成都七中实验学校高一3月月考数学试卷(解析版) 题型:选择题
1202年,意大利数学家斐波那契在他的书中给出了一个关于兔子繁殖的递推关系: (
( ),其中
),其中 表示第
表示第 个月的兔子的总对数,
个月的兔子的总对数, ,则
,则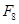 的值为( )
的值为( )
A.13 B.21 C.34 D.55
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省中山市高二(上)期末数学试卷(文科)(解析版) 题型:选择题
 由此可计算出F7=( )
由此可计算出F7=( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com